[머피 머신러닝] Chapter 1. Introduction

1. Machine learning: what and why?

• 머신 러닝 정의: 데이터 속에서 숨겨진 패턴을 찾고, 패턴을 이용해서 데이터를 예측하는 방법론

 

1-1. 머신러닝 유형

지도학습(predictive / supervised learning)

• 목표: 입력 데이터(x)로 부터 결과 데이터(y)을 예측하는 모델을 학습하는 것
• 데이터셋이  $ D={\left ( x_{i}, y_{i} \right )}_{i=1}^{N} $ 로 학습을 위해 입력데이터와 결과데이터가 필요함

 

• 문제 유형
  1. 분류(classification): 결과 데이터가 범주화된 경우 (categorical)
  2. 회귀(regression):  결과 데이터가 수치인 경우 (real-valued)

 

• 결과 데이터(y)를 예측하기 위해 입력 데이터(x)를 이용해 근사 함수 (Function approximation)를 학습한다.
• 우리가 모르는 함수 y = f(x)로 인해 결과 데이터가 나온다고 가정할 시, 근사함수 $ \widehat{y} = \widehat{f}\left ( x \right ) $를 학습해 일반화(generalization) 하는 것

 

 

비지도학습 (descriptive / unsupervised learning)

• 목표: 데이터로부터 유의미한 패턴을 찾는 것
• 데이터셋이  $ D={\left ( x_{i}  \right )}_{i=1}^{N} $ 로 학습을 위한 데이터만 존재함
• 지도학습과 다르게 예측해야 되는 목표가 없다. 즉, 데이터 속 숨겨진 패턴을 찾아야한다 (knowledge discovery)
• 데이터 패턴은 특정 확률 $ p \left ( x_{i} | \theta \right ) $로 인해 발생하는 density estimation 개념으로 볼 수 있다.
• 결과 데이터를 얻는데 비용이 많이 들어 input data의 패턴만으로 결과를 추정하고자 할 때에도 사용될 수 있다.

 

강화학습 (reinforcement learning)

• 어떤 행동을 할 때 보상이나 처벌이 주어진다고 할 때, 어떻게 행동하는 것이 최선인지 학습하는 방법론

 

 

2. Supervised learning

분류 (Classification)

• 범주형 (categorical) 변수인 y를 예측하는 방법론
• $  y \in \left\{1, ..., C \right\} $
  • 이진 분류(binary classification): C = 2일 때
  • 다중 분류(multiclass classfication): C > 2 일 때

 

 

• 확률론적 관점으로 표현할 수 있다.
  • $ p\left ( y|x, D \right ) $: x와 D가 주어질 때 y의 조건부 확률
  • $ \hat{y} = \hat{f}\left ( x \right ) = {argmax}_{c=1}^{C}p\left ( y=c|x, D \right ) $ 를 통해 학습 모델을 표현할 수 있다.
  • 위 수식은 데이터가 주어질 때 y에 대한 사후 확률을 최대화 하기 때문에MAP(Maximum A Posteriori) estimate로 불린다.

 

• 현실에서 사용되는 사례
  • 문서 분류
  • 이메일 스팸 필터링
  • 이미지 분류및 인식
  • 안면 인식

 

회귀 (Regression)

• 실수 (real-value) 변수인 y를 예측하는 방법론
• $ y_{i} \in \mathbb{R} $

 

3. Unsupervised learning

군집화 (clustering)

• 데이터가 어느 집단에 속할지를 예측하는 방법
• $ K^{*} = argmax_{K}p\left ( K|D \right ) $

 

• $ z_{i} \in \left\{ 1, ..., K\right\} $
  • 집단의 개수를 몇개로 설정할 것인지, 즉 모델의 복잡도 (complexity)는 분석자가 임의로 설정할 수 있다.

 

• $ z_{i}^{*} = argmax_{k}p\left ( z_{i} = k |x_{i}, D \right ) $
  • 관측치(point)가 어느 클러스터에 속할지 계산

 

 

잠재 요인 (Latent factors)

• 차원 축소(dimensionality reduction): 고차원 데이터에서 의미 있는 저차원 공간(subspace)로 투영(projection)하는 방법
  • 고차원 공간 속에서 의미있는(essential) 잠재 요인(latent factor)들은 한정적이다는 것을 가정
  • 고차원 공간을 축소하여 성능을 높이거나 효과적인 시각화를 가능케함

 

 

• PCA (Principle Component Analysis)
  • 가장 대표적인 차원축소 방법
  • $  z \to y $
  • z: 저차원 공간
  • y: 고차원 공간

 

 

그래프 (Graph)

• 그래프 구조로 관련있는 변수간 관계를 나타낸 것
  • node: 변수
  • edge: 변수간의 관계

 

• $ \hat{ G} = argmaxp\left ( G|D \right ) $

 

행렬 문제 (Matrix Completion)

• 데이터 내 결측 값(missing entries)이 있을 때 적합한 값으로 채워넣는 것 (imputation)

 

• use case
  • Image inpainting
  • Collaborative filtering
  • Market basket analysis

 

 

 

4. Some basic concepts in machine learning

매개변수 모델 (Parametric model)

• 모델의 매개변수의 개수 (모델의 크기)가 정해져있다.
• 장점: 학습 및 사용이 빠르다.
• 단점: 매개변수의 크기를 정해야 한다 (사용자가 데이터셋의 크기, 데이터 분포 등을 미리 파악하고, 복잡도를 설정해야 한다)

 

 

비매개변수 모델 (Non-Parametric model)

• 데이터 크기에 따라 매개변수의 개수 (모델의 크기)가 변할 수 있다.
• 장점: 데이터 크기에 상관없이 유연하게 사용할 수 있다.
• 단점: 큰 데이터셋에서 학습하기 어려울 수 있다.

 

 

K-최근접 이웃 알고리즘 (K-nearest neighbor algorithm)

• 비매개변수 모델 중 가장 대표적인 알고리즘
• 테스트 데이터 x에서 가장 가까운 K개 데이터를 학습셋에서 가져와서 예측함

 

• $  p\left ( y=c| \boldsymbol{x}, D, K \right )=\frac{1}{K}\sum_{i\in N_{K}\left ( \boldsymbol{x} ,D \right )}\mathbb{I}\left ( y_{i}=c \right ) $
  • $ N_{K}\left (\boldsymbol{x},D  \right ) $는 학습셋(D) 내에서 x와 가까운 K개의 point들
  • $ \mathbb{I}\left ( e \right ) $: indicator function 으로 e가 참이면 1, e가 거짓이면 0
• memory-based / instance-based learning 방식이다.

 

• K-NN으로 분류 시, 데이터 수가 무한대에 가까워질수록 최고의 성능을 낼 수 있다.
  • 관측 데이터가 많을수록 차원 내 빈공간이 사라지기 때문

 

 

차원의 저주 (The curse of dimensionality)

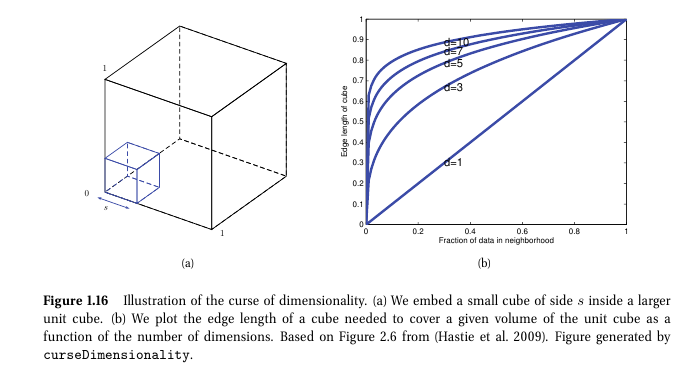
• 차원이 증가할수록 테스트 데이터를 설명할 학습 데이터
• 관측치 수에 비해 변수 수가 많아질수록 문제가 된다.
  • 차원이 늘어날수록 관측치들간 빈 공간(sparse)가 커지기 때문

 

 

선형 회귀 (Linear regression)

• 매개변수 모델 중 하나
• 주어진 데이터들로 선형 함수를 생성해 output을 예측

 

• $ y\left ( x \right ) = w^{T}x + \varepsilon = \sum_{j=1}^{D}w_{j}x_{j}+\varepsilon  $
  
  • $ \varepsilon \sim \mathit{N}\left ( y|\mu \left ( x \right ), \sigma ^{2}\left ( x \right ) \right ) $

 

• $ p\left ( y|x, \theta  \right ) = \mathit{N}\left ( \mu \left ( x \right ), \sigma ^2\left ( x \right ) \right ) $
  • 여기서 $ \mu \left ( x \right )= w_{0} + w_{1}x = w^{T}x $

 

 

로지스틱 회귀 (Logistic regression)

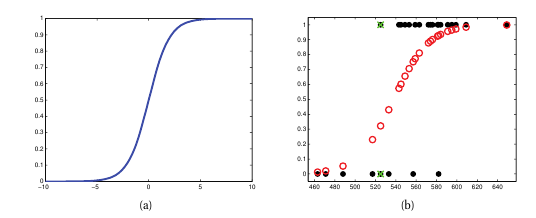
• 매개변수 모델이며 실제로는 classification 모델임

 

• 선형 회귀에서 아래 가정으로 변경
  1. $ p\left ( y|x, w \right ) = Ber\left ( y|\mu \left ( x \right ) \right ) $
     • $ \mu \left ( x \right )=\mathbb{E}[y|x]=p\left ( y=1|x \right ) $
     • $ 0\leq \mu \left ( x \right ) \leq 1 $
  2. $ \mu \left ( x \right )= sigm\left ( w^Tx \right ) $
     • $ sigm\left ( \eta  \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{1+exp\left ( -\eta  \right )}=\frac{e^\eta }{e^\eta +1} $

 

• 최종 식: $ p\left ( y|x,w \right ) = Ber\left ( y|sigm\left ( w^Tx \right ) \right ) $

 

과적합 (Overfitting)

• 모델이 데이터 내 존재하는 패턴보다는 노이즈에 대해서 학습이 될 때
• 데이터가 제공하는 정보보다 모델의 사이즈가 더 커서 variation이 심한 경우다.

 

 

모델 선택

• 일부 데이터셋에 대한 성능으로 모델을 선택
• underfit / overfit 여부 체크
• 학습/테스트셋 외에 검증셋을 통한 성능 평가
  • Cross validation (CV)
  • LOOCV(Leave-One Out Cross Validation)

 

 

최선의 선택은 없다.

• 모든 데이터에 대해서 최고의 성능을 내는 모델은 없다.
• 최선의 모델이 데이터, 도메인별로 다를 수 있다.