[머피 머신러닝] Chapter 3. Generative models for discrete data

1. Introduction

$  p\left ( y=c|x,\theta \right )\propto p\left ( x|y=c,\theta \right )p\left ( y=c|\theta \right ) $

• 베이즈룰에 따른 generative classifier
• 여기서 $ p\left ( x|y=c, \theta \right ) $ 인 class-conditional density를 어떻게 적절한 형태로 표현할지가 핵심 사항

 

 

 

2. Bayesian concept learning

ㄱ. 개념 학습(concept learning)

• 이진 분류(binary classification)와 유사
• x가 concept C에 속하면 f(x) = 1이고, 아니면 f(x) = 0
• 어떤 요소들이 C 개념에 속하는지 판단하는 지시함수 (indicator function; $ f\left ( \cdot  \right ) $)을 학습하는 것이 목표이다.
• 이진 분류는 참과 거짓인 예제들로 학습하는 것과 달리, 개념 학습은 참인 예제들로만 학습함

 

• $  p\left ( \tilde{x}|D \right ) $: 사후 확률 분포
  • 데이터셋 D가 주어졌을 때, $ \tilde{x}\in C $ 일 확률

 

관측 데이터에 따라 사후확률분포가 달라지게 된다.

 

• 귀납(induction)
  • 주어진 관측들을 통해 결과를 이끌어 내는 방법
  • ex> {2, 4, 8, 64} 로 이루어진 관측들을 보니 2의 거듭제곱 집합으로 볼 수 있다.

 

• 가설 공간 (hypothesis space, $ \mathfrak{H} $)
  • 귀납적으로 어떤 사건이나 현상을 가정한 공간

 

• Version space
  • 가설 공간 H의 하위 집합
  • 데이터 D에 따라 나타날 수 있는 version space가 다양할 수 있다.
  • 관측이 많아질수록 version space는 줄어들고, 개념(concept)에 대해 더 확실해진다.

 

• Bayesian이 관측 결과들을 통해 어떻게 해석하는지를 공부해보자.

 

 

2-1. 우도

관측들을 통해 여러 가정이 발생할 수 있는데, 여기서 의심스러운 우연 (suspicious coincidence)을 어떻게 피할 것인가?

 

ㄱ. strong sampling assumption

$ p\left ( D|h \right )=[\frac{1}{size\left ( h \right )}]^N=[\frac{1}{|h|}]^N $

• 가설 공간에서 샘플들이 뽑힐 확률은 모두 같다고 가정
• 가설 공간에서 해당 관측 결과가 나올 확률은 얼마인지 계산
• Ocacam's razor: 모델링은 데이터를 통해 가장 간단한 가정을 선호한다.

 

관측 결과 우도(likelihood)가 어느 가정에서 가장 높은지 비교 -> 확률적으로 더 적합한 가설공간을 선택할 수 있다.

 

 

2-2. 사전 확률

ㄱ. 사전 확률(prior)

• 개념이 특정 가설일거라 생각하는 주관적 확률
• 자연스럽지 않은 개념들에 대해서는 낮은 사전확률(prior)을 줘서 배제할 수 있음
• 분석가에 따라 주관적인 관점이 들어간다는 측면에 대해서 베이지안 추론(Bayesian reasoning)의 결과가 달라질 수 있다는 논란이 있다.
• 논란이 있는 가설들에 대해서는 사전 확률의 비중을 조절하여 조정할 수 있다.
• 해당 사건에 대한 기존 배경 지식이 모델링에 도움을 줄 수 있다는 판단

 

 

2-3. 사후 확률

ㄱ. 사후 확률(Posterior)

$ p\left ( h|D \right )=\frac{p\left ( D|h \right )p\left ( h \right )}{\sum _{h'\in \mathfrak{H}}p\left ( D,h' \right )}=\frac{p\left ( h \right )\mathbb{I}\left ( D\in h \right )/|h|^N}{\sum _{h'\in \mathfrak{H}}p\left ( h' \right )\mathbb{I}\left ( D\in h' \right )/|h'|^N} $

• 우도와 사전확률의 곱을 표준화한 것
• $ \mathbb{I}\left ( D\in h \right ) $ = 1: iff 모든 데이터가 가설 공간 h에 속할 때
• 비정상적인 가설 공간에는 낮은 사전확률 값을 준다: 우도가 높더라도 모델이 데이터에 overfitting 되는 현상을 막을 수 있음 

 

 

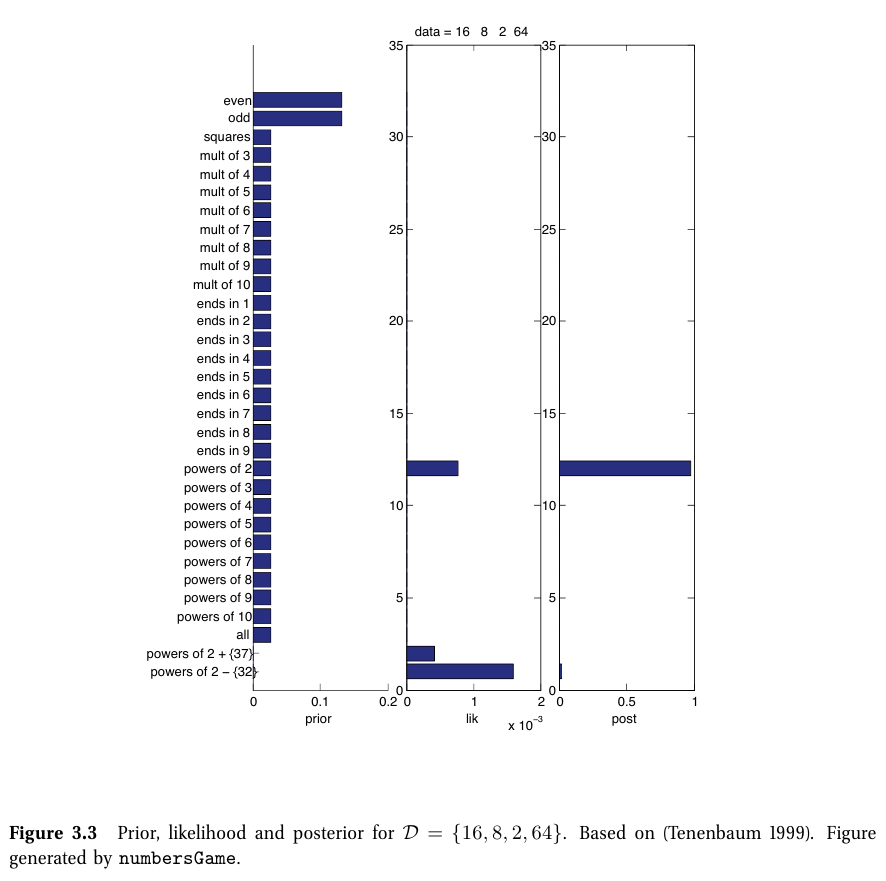
ㄴ. 낮은 사후 확률이 나올 때

1. 높은 사전 확률, 낮은 우도
2. 낮은 사전 확률, 높은 우도
3. others

 

ㄷ. MAP (Maximum A Posteriori)

$ p\left ( h|D \right )\to \delta_{\hat{h}^{MAP}}\left ( h \right ) $

• 충분한 데이터는 사후 확률 $ p\left ( h|D \right ) $을 단일 개념에 수렴하게 한다.
• $ \hat{h}^{MAP}=\textrm{argmax}_{h}p\left ( h|D \right ) $: posterior mode
• $ \delta $: Dirac measure
  • 1 if $ x \in A $
  • 0 if $ x \notin A $

 

ㄹ. MAP estimate

$ \hat{h}^{MAP}=\textrm{argmax}_{h}p\left ( D|h \right )p\left ( h \right )=\textrm{argmax}_h[ \textrm{log}p\left ( D|h \right )+ \textrm{log}p\left ( h \right )] $

• 우도는 관측 수(N)에 기하급수적으로 커고, 사전확률은 상수임
• 따라서 데이터가 많을수록 MAP는 MLE로 수렴하게 됨
• 즉, 데이터가 많으면 사전확률은 무시할 수 있게 됨

 

ㅁ. MLE (Maximum Likelihood Estimate)

$ \hat{h}^{mle}\overset{\underset{\mathrm{def}}{}}{=}\textrm{argmax}_hp\left ( D|h \right )=\mathrm{argmax}_h\textrm{log}p\left ( D|h \right ) $

• 무한한 데이터가 있으면 가설 공간 속 참 가설을 찾을 수 있다 (identifiable in the limit)
• 가설 공간 내 참 가설이 없으면 참 가설과 가장 가까운 가설로 수렴하게 된다.

 

ㅂ. 사후확률 정리

• MLE
  • likelihood를 maximize 시켜 추정
  • 관측 결과에 민감
  • 관측의 양과 질에 크게 좌우
  • 우도만 반영
  • 관측 수가 클수록 사전 확률이 큰 의미가 없어짐.

 

•  MAP
  • Posterior를 maximize 시켜 추정
  • 사전확률이 반영된 추정치로 분석가의 주관적 의견이 반영될 수 있음
  • 사전 확률 반영
  • 데이터 수가 적을 때 사전확률이 특정 가정들로 선택되는데 영향을 미칠 수 있다.

 

• $ MAP \to MLE $
  • 사전확률이 모두 uniform distribution인 경우
  • $ N\to \infty $

 

 

2-4. 사후 예측 분포

ㄱ. 사후 예측 분포 (posterior predictive distribution)

1) 베이지안 모델 평균 (Bayes model averaging)

$ p\left ( \tilde{x}\in C|D \right )=\sum _{h}p\left ( y=1|\tilde{x},h \right )p\left ( h|D \right ) $

• 각 개별 가설의 확률에 대한 가중 평균

 

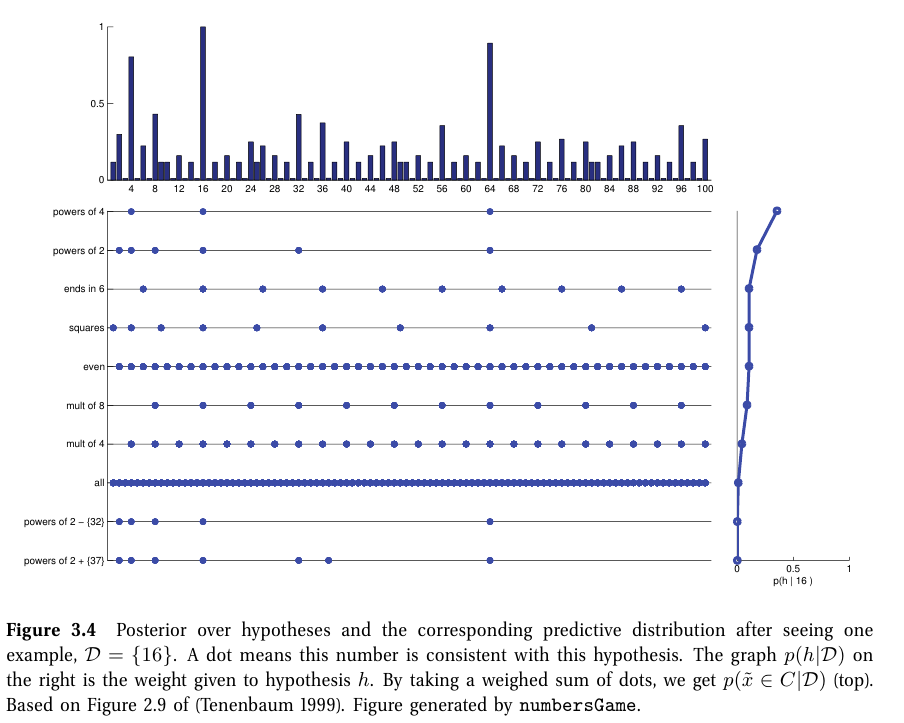
[그림]

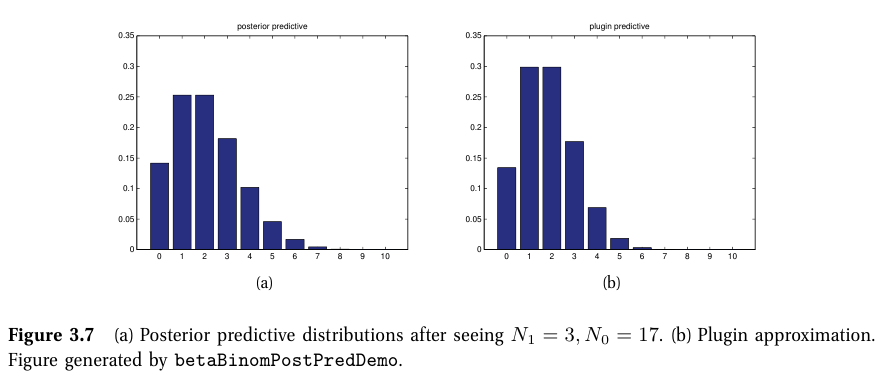
• 적은 데이터셋: 사후확률 $ p\left ( h|D \right ) $은 모호하며, 광범위한 예측 분포를 가짐
• 많은 데이터셋: MAP distribution에서 사후확률은 delta function으로 표현할 수 있음 -> plug-in approximation으로 표현 가능

 

2) 플러그인 근사(plug-in approximation)

$ p\left ( \tilde{x}\in C|D \right )=\sum _{h}p\left ( \tilde{x}|h \right )\delta_{\hat{h}}\left ( h \right )=p\left ( \tilde{x}|\hat{h} \right ) $

• 장점: 간단하게 가정
• 단점: 불확실성을 과소 평가하며, 베이지안 모델 평균에 비해서 다른 가정들을 반영하지 못함

 

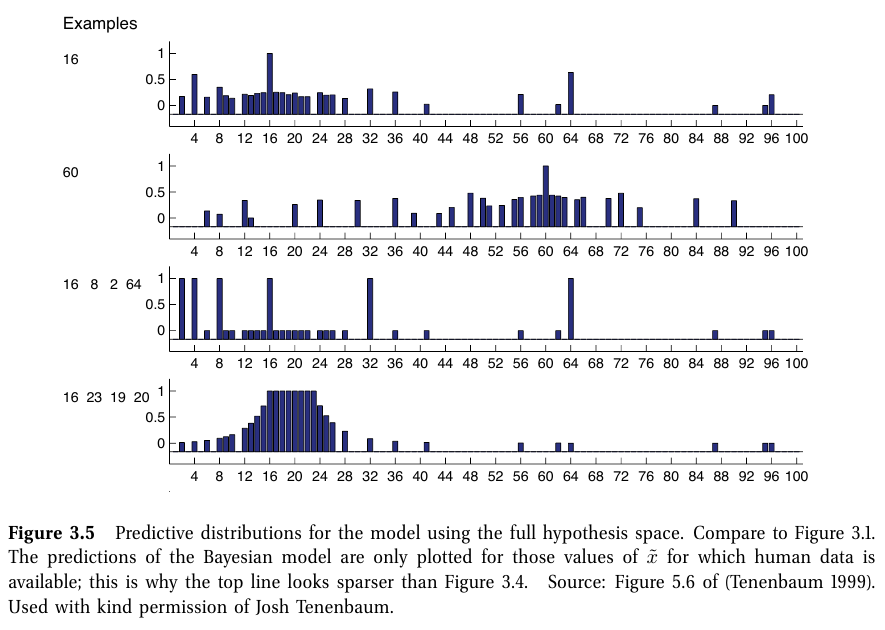
3) 베이지안 모델 평균 vs 플러그인 근사

• 베이지안 모델 평균: 데이터를 관측할수록 넓은 가설 공간에서 점점 좁아짐
• 플러그인 근사: 데이터를 관측할수록 가설공간에 대한 좁은 가정이 넓어질 수 있음
• 결국 데이터 수가 많아지면 둘다 같은 답으로 수렴한다.

 

 

2-5. 더 복잡한 사전 확률

ㄱ. mixure of two prior

$ p\left ( h \right )=\pi_0p_{\textrm{rules}}\left ( h \right )+\left ( 1-\pi_0 \right )p_{\textrm{interval}}\left ( h \right ) $

 

 

3. The beta-binomial model

3-1. 우도

ㄱ. 베르누이 분포

$  X_i \sim \textrm{Ber}\left ( \theta \right ) $

• $ \theta \in [0, 1] $: rate parameter

 

ㄴ. 베르누이 분포 우도

$ p\left ( D|\theta \right )=\theta^{N_1}\left ( 1-\theta \right )^{N_0} $

• $ N_k=\sum_{i=1}^{N}\mathbb{I}\left ( x_i=k \right ) $ (여기서 k = 0 or 1)
  • sufficient statistics: $ \theta $를 추론하기 위해 데이터 D에 대해 알아야할 통계량 (여기서는 $ N_0, N_1 $)
  • $ s\left ( D \right ) $ 로 표현할 수 있으며, $ p\left ( \theta | D \right ) = p\left ( \theta|s\left ( data \right ) \right ) $

 

ㄷ. 이항 분포

$ \textrm{Bin}\left ( k|n,\theta \right )\overset{\underset{\mathrm{def}}{}}{=}\binom{n}{k}\theta^k\left ( 1-\theta \right )^{n-k} $

• $ \binom{n}{k} $: $ \theta $와 독립적인 상수항
• likelihood는 베르누이분포와 동일하다.

 

 

3-2. 사전 확률

$ p\left ( \theta \right ) \propto \theta^{\gamma_1}\left ( 1-\theta \right )^{\gamma_2} $

• 계산의 편리성을 위해 사전확률은 우도와 동일한 형태를 띄고 있는게 편하다.

 

$ p\left ( \theta \right )\propto p\left ( D|\theta \right )p\left ( \theta \right )=\theta^{N_1}\left ( 1-\theta \right )^{N_0}\theta^{\gamma_1}\left ( 1-\theta \right )^{\gamma_{2}}=\theta^{N_1+\gamma_1}\left ( 1-\theta \right )^{N_0+\gamma_2} $

• 사후 확률은 단순히 지수합을 통해서 나타낼 수 있다.
• 켤레 사전확률(conjugate prior): 사전확률이 사후확률이 같은 형태를 띄고 있을 때
• 켤레 사전확률은 계산상 편리함과 해석의 용이함으로 자주 사용된다.

 

ㄱ. 베르누이 분포

$ \textrm{Beta}\left ( \theta|a, b \right )\propto \theta^{a-1}\left ( 1-\theta \right )^{b-1} $

• 베르누이 분포의 켤레 사전확률는 베타 분포
• 초매개변수(hyper-parameters): 사전확률의 파라미터를 지칭
  • 초매개변수는 사전확률에 대한 분석가의 판단으로 설정
  • uninformative prior: $ \theta $에 대한 정보를 모를 때 uniform prior를 줄 수 있다 (a=b=1).

 

3-3. 사후 확률

$ p\left ( \theta|D \right )\propto \textrm{Bin}\left ( N_1|\theta,N_0+N_1 \right )\textrm{Beta}\left ( \theta|a,b \right )\propto  \textrm{Beta}\left ( \theta|N_1+a,N_0+Bb \right ) $

• 사후확률은 관측 값(empirical counts)과 사전확률 초매개변수의 합으로 얻어진다.
• 즉, 사후확률은 사전확률과 우도 사이에서 절충된다.
• pseudo counts: 사전확률의 초매개변수는 가짜 관측 값으로 볼 수 있다.
• effective sample size of the prior: 사후확률에 영향을 미치는 사전확률의 영향도

 

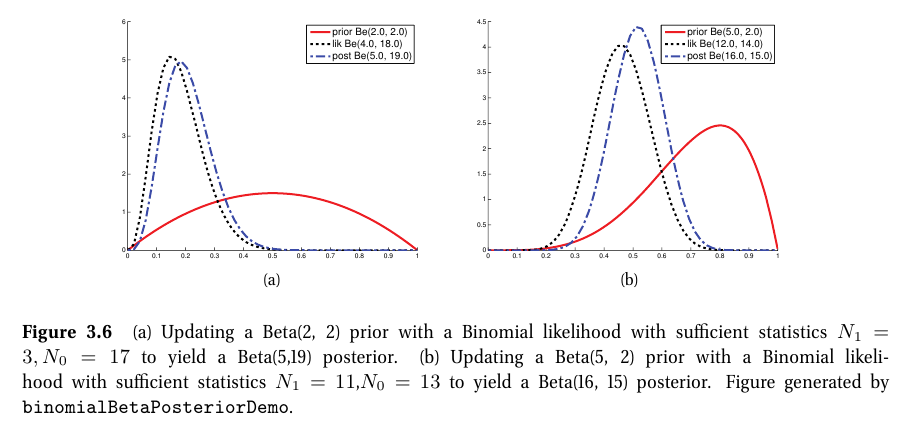
ㄱ. 사후확률 갱신(update)

$ \textrm{Bin}\left ( N_1^{new}|\theta, N_1^{new} + N_0^{new} \right )\textrm{Beta}\left ( \theta|N_1^{old}+a, N_0^{old}+b \right ) $

• 새로운 관측 (Binomial 분포) 에 대해서 기존 관측 + prior (Beta 분포)를 곱해서 사후 확률을 갱신할 수 있다.
• online learning: 실시간으로 모델 재학습/업데이트

 

사후확률 갱신 (a -> b)

 

ㄴ. 사후 확률 평균

$ \bar{\theta}=\frac{a+N_1}{a+b+N} $

• 사후 확률 평균은 사전 확률 평균과 MLE 사이의 convex combination이다.

 

$ E[\theta|D]=\frac{\alpha_0m_1+N_1}{N+\alpha_0}=\frac{\alpha_0}{N+\alpha_0}m_1+\frac{N}{N+\alpha_0}\frac{N_1}{N}=\gamma m_1 + \left ( 1-\gamma \right )\hat{\theta}_{MLE} $

• $ \alpha_0=a+b $: equivalent sample size of the prior (prior의 영향력)
• $ m_1=a/\alpha_0 $: 사전확률 평균
• $ \gamma=\frac{\alpha_0}{N+\alpha_0} $: 사후확률에 대한 사전 확률의 샘플 크기
  • 사전 확률 영향력이 작아질수록 $ \gamma $ 크기가 작아지고, 사후확률 평균은 MLE에 수렴한다.

 

ㄷ. 사후 확률 최빈값

• 사후확률 평균과 같이 사전 확률 최빈값과 MLE의 convex combination이다.

 

ㄹ. 사후 확률 분산

$ var[\theta|D]=\frac{\left ( a+N_1 \right )\left ( b+N_0 \right )}{\left ( a+N_1+b+N_0 \right )^2\left ( a+N_1+b+N_0+1 \right )} $

• 베타 사후확률의 분산

 

$ var[\theta|D]\approx \frac{N_1N_0}{NNN}=\frac{\hat{\theta}\left ( 1-\hat{\theta} \right )}{N} $

• $ \hat {\theta} $: MLE

 

ㅁ. 사후 확률 표준편차

$ \sigma = \sqrt{var[\theta|D]}=\sqrt{\frac{\hat{\theta}\left ( 1-\hat{\theta} \right )}{N}} $

• 불확실성은 $ 1/\sqrt{N} $으로 내려간다.
• $ \hat {\theta} = 0.5$일 때 불확실성은 최대화되고, $ \hat {\theta} $가 0이나 1일 때 최소가 된다.

 

 

3-4. 사후 예측 분포

$ p\left ( \tilde{x}=1|D \right )=\int _0^1p\left ( x=1|\theta \right )p\left ( \theta|D \right )d\theta=\int_0^1\theta \textrm{Beta}\left ( \theta|a,b \right )d\theta=\mathbb{E}[\theta|D]=\frac{a}{a+b} $

• $ p\left ( \tilde{x}|D \right )=\textrm{Ber}\left ( \tilde{x}|\mathbb{E}[\theta|D] \right ) $
• 여기서 적은 관측치로 계산된 MLE를 사후 예측 확률로 간주하면 overfitting될 수 있다.
  • N = 3, $ \hat {\theta} = 0/3 = 0$ 일 때 문제가 생길 수 있음
  • 이 때는 사전 확률에 대해 uniform prior (a=b=1)를 주면 해결할 수 있음

 

ㄱ. beta-binomial 분포

• M번 시행되는 동전던지기에서 앞면이 나올 확률 분포

 

Plugin 접근보다 좀 더 강건하다 (overfitting 방지)

 

 

4. The Dirichlet-multinomial model

4-1. 우도

$  p\left ( D|\theta \right )=\prod_{k=1}^{K}\theta_{k}^{N_k} $

• $ D=\left\{ x_1, \cdots , x_N\right\} $
• $ x_i\in \left\{ 1, \cdots , K\right\} $
• $ N_k=\sum_{i=1}^{N}\mathbb{I}\left ( y_i=k \right ) $: 사건 k가 일어난 횟수

 

4-2. 사전 확률

$ \textrm{Dir}\left ( \theta|\alpha \right )=\frac{1}{B\left ( \alpha \right )}\prod_{k=1}^{K}\theta_k^{\alpha_k-1}\mathbb{I}\left ( x\in S_K \right ) $

 

4-3. 사후 확률

$ p\left ( \theta|D \right ) \propto p \left ( D|\theta \right )p\left ( \theta \right ) $

$ \propto \prod_{k=1}^{K}\theta_k^{N_k}\theta_k^{\alpha_k-1}=\prod_{k=1}^{K}\theta_k^{\alpha_k+N_k-1} $

$ = \textrm{Dir}\left ( \theta|\alpha_1+N_1, \cdots, \alpha_N+N_K \right ) $

• $ \alpha_k $: 사전확률 초매개변수 (가짜 관측 수)
• $ N_K $: 실제 관측 수

 

ㄱ. 라그랑주 승수법 (Lagrange multiplier)

$ \mathit{l}\left ( \theta, \lambda \right )=\sum _kN_k\textrm{log}\theta_k+\sum _k\left ( \alpha_k-1 \right )\textrm{log}\theta_k+\lambda\left ( 1-\sum_k\theta_k \right ) $

• $ \sum _k\theta_k = 1 $
  • 라그랑주 승수법을 이용해 제약
  • log likelihood와 log prior에 제약식을 더해준다.

 

4-4. 사후 예측 분포

ㄱ. 단일 멀티누이 시행

$ p\left ( X=j|D \right )=\int p\left ( X=j|\theta \right )p\left ( \theta|D \right )d\theta $

$ = \int p\left ( X=j|\theta_j \right )[\int p\left ( \theta_{-j},\theta_j|D \right )d\theta_{-j}]d\theta $

$ = \int \theta_jp\left ( \theta_j|D \right )d\theta_j=\mathbb{E}[\theta_j|D]=\frac{\alpha_j+N_j}{\sum_k\left ( \alpha_k+N_k \right )}=\frac{\alpha_j+N_j}{\alpha_0+N} $

• $ \theta_{-j} $: $ \theta_j $를 제외한 $ \theta $의 모든 요소
• $ \frac{\alpha_j+N_j}{\sum_k\left ( \alpha_k+N_k \right )} $에서 zero-count 문제 (관측이 없어서 확률이 0이되는 경우)를 피한다.

 

 

5. Naive Bayes classifier

ㄱ. Naive Bayes Classifier(NBC)

$ p\left ( \textbf{x}|y=c, \boldsymbol{\theta} \right )=\prod_{j=1}^{D}p\left ( x_j|y=c, \boldsymbol{\theta}_{jc} \right ) $

• $ \textbf{x}\in\left\{ 1,\cdots, K\right\}^D $
• 특성(feature)들은 클래스에 대해서 조건부 독립이라고 naive하게 가정 (실제 현실에서는 feature들간 독립을 보장할 수 없다.)
• 실제 모델링에서는 잘 동작하는 편.

 

1) 실수(real-valued) 특성인 경우

•  가우시안 분포를 사용할 수 있다.

 

2) 이항 특성인 경우

• 베르누이 분포를 사용

 

3) 범주형 특성인 경우

• 멀티누이 분포를 사용

 

 

5-1. 모델 학습

MLE나 MAP를 계산하면 된다.

 

ㄱ. MLE 계산

$ p\left ( x_i,y_i|\theta \right )=p\left ( y_i|\pi \right )\prod_j p\left ( x_{ij}|\theta_j \right )=\prod_c \pi_c^{\mathbb{I}\left ( y_i=c \right )}\prod_j \prod_c p\left ( x_{ij}|\theta_{jc} \right )^{\mathbb{I}\left ( y_i=c \right )} $

 

1) log-likelihood

단어 j가 발생 시 어느 클래스에 속할지에 대한 우도

$ \textrm{log}p\left ( D|\theta \right )=\sum_{c=1}^{C}N_c\textrm{log}\pi_c+\sum_{j=1}^{D}\sum_{c=1}^{C}\sum_{y_i=c}\textrm{log}p\left ( x_{ij}|\theta_{jc} \right ) $

 

2) class prior

$ \hat{\pi}_c=\frac{N_c}{N} $

• 여기서 $ N_c $는 클래스 c에 속하는 관측 수

 

$ \hat{\theta}_{jc}=\frac{N_{jc}}{N_c} $

• 모든 특성들이 binary라고 가정하고 베르누이 분포를 띈다고 할 때 MLE
• O(ND)

 

3) 알고리즘 pseudo-code

ㄴ. Baysian naive Nayes

MLE는 overfitting 될 수 있다 (관측되지 않은 것에 대해서는 예측할 수 없다).

=> Bayesian을 통해 MLE의 overfitting을 피하는 방법

 

 

1) factored prior

$ p\left ( \theta \right )=p\left ( \pi \right )\prod_{j=1}^D\prod_{c=1}^{C}p\left ( \theta_{jc} \right ) $

• $ \textrm{Dir}\left ( \alpha \right ) $: $ \pi $에 대한 사전분포
• $ \textrm{Beta}\left ( \beta_0, \beta_1 \right ) $: $ \theta_{jc} $에 대한 사전분포

 

2) factored posterior

$ p\left ( \theta|D \right )=p\left ( \left ( \pi|D \right ) \right )\prod_{j=1}^{D}\prod_{c=1}^{C}p\left ( \theta_{jc}|D \right ) $

$ p\left ( \pi|D \right )=\textrm{Dir}\left ( N_1+\alpha_1,\cdots ,N_C+\alpha_C \right ) $

$ p\left ( \theta_{jc}|D \right )=\textrm{Beta}\left ( \left ( N_c-N_{jc} \right )+\beta_0, N_{jc}+\beta_1 \right ) $

• factored prior와 factored likelihood를 이용

 

5-2. 예측에 모델을 사용

$ p\left ( y=c|x,D \right )\propto p\left ( y=c|D \right )\prod_{j=1}^Dp\left ( x_j|y=c,D \right ) $

$ \propto [\int \textrm{Cat}\left ( y=c|\pi \right )p\left ( \pi|D \right )d\pi]\prod_{j=1}^{D}[\int \textrm{Ber}\left ( x_j|y=c,\theta_{jc} \right )p\left ( \theta_{jc}|D \right )] $

• 위 산식을 통해 주어진 x가 어느 클래스에 속할 확률이 가장 높은지 확인

 

 

5-3. The log-sum-exp trick

$  p\left ( y=c|x,\theta \right )=\frac{p\left ( y=c|\theta \right )p\left ( x|y=c,\theta \right )}{\sum_{c'}p\left ( y=c'|\theta \right )p\left ( x|y=c',\theta \right )} $

• 사후 확률은 numerical underflow로 인해서 계산에 실패할 수 있다.
• x가 고차원 벡터인 경우, $ p\left ( x|y=c \right ) $가 아주 작은 값이 될 수 있기 때문
• 확률 값이 엄청 작아지는 경우를 log-sum을 통해 보완하자!

 

ㄱ. log-sum-exp trick

$ \textrm{log}p\left ( y=c|x \right )=b_c-\textrm{log}[\sum_{c'=1}^Ce^{b_{c'}}] $

• $ b_c\overset{\underset{\mathrm{def}}{}}{=}\textrm{log}p\left ( x|y=c \right )+\textrm{log}p\left ( y=c \right ) $
• $ \textrm{log}[\sum_{c'}e^{b_{c'}}]=\textrm{log}\sum_{c'}p\left ( y=c',x \right )=\textrm{log}p\left ( x \right ) $
  • log 관점에서 합산 값을 구할 수 없다 => 가장 큰 항목을 이용해서 값을 빼내자!
  • $ \textrm{log}\sum_c e^{b_c}=\textrm{log}[\left ( \sum_c e^{b_c-B} \right )e^B]=[\textrm{log}\left ( \sum_c e^{b_c-B} \right )]+B $
  • 여기서 $ B = \textrm{max}_c b_c $

 

 

 

5-4. 상호 정보를 이용한 변수 선택

ㄱ. NBC의 단점

1) 모든 변수들에 대해서 결합확률로 표현되기 때문에 overfitting 가능성 존재

2) 실행 비용 O(D)가 부담스러울 수 있다.

 

ㄴ. 변수 선택(feature selection)

• 분류 문제에 도움을 주는 변수들만을 선택하는 방법
• ranking(filtering or screening): 분류 문제에 가장 도움이되는 K개의 변수들만을 선택하는 방법

 

ㄷ. 상호 정보를 이용한 변수 영향도 측정 방법

$ I\left ( X,Y \right )=\sum_{x_j}\sum_{y}p\left ( x_j,y \right )\textrm{log}\frac{p\left ( x_j,y \right )}{p\left ( x_j \right )p\left ( y \right )} $

• 특성 j를 관측했을 때 라벨 분포에 대한 엔트로피가 얼마나 감소하는지로 해석할 수 있다.
• 상호정보량이 큰 특성 j가 클래스를 분별하는데 더 도움이 됨 (단순히 많이 나오는 특성은 클래스 분별에 의미가 없음)

 

 

5-5. bag of words를 이용한 문서 분류

ㄱ. 문서 분류(Document classification)

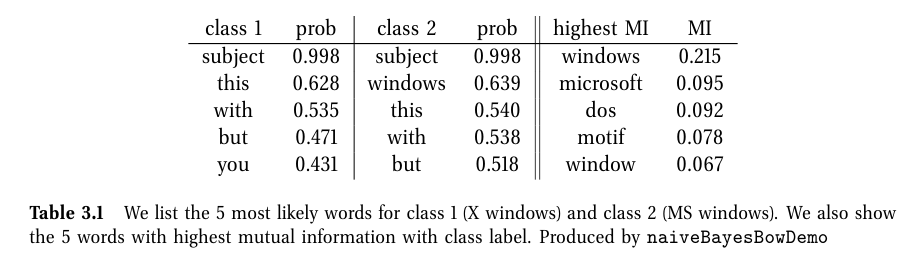
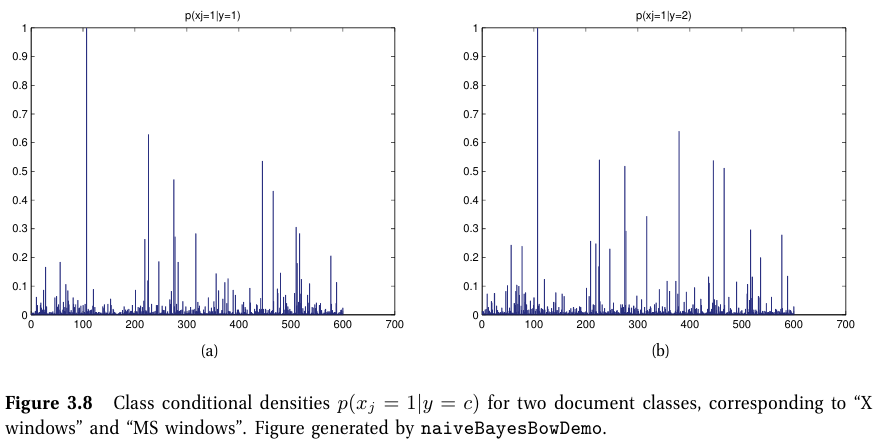
• 텍스트 문서를 카테고리로 분류하는 문제

 

ㄴ. 베르누이 곱 모델(Bernoulli product model or binary independence model)

$ p\left ( x_i|y_i=c,\theta \right )=\prod_{j=1}^D\textrm{Ber}\left ( x_{ij}|\theta_{jc} \right )=\prod_{j=1}^D\theta_{jc}^{\mathbb{I}\left ( x_{ij} \right )}\left ( 1-\theta \right )^{\mathbb{I}\left ( 1-x_{ij} \right )} $

• 단순히 문서 내에 특정 단어 j가 문서 i에서 나왔는지를 나타내는 이진벡터로 분류
• 단어 빈도를 체크하는 multinoulli 모델도 있지만 성능상 한계가 있다 (burstiness phenomenon).

 

ㄷ. Dirichlet Compound Multinomial (DCM) density

$ p\left ( x_i|y_i=c,\alpha \right )=\int \textrm{Mu}\left ( x_i|N_i,\theta_c \right )\textrm{Dir}\left ( \theta_c|\alpha_c \right )d\theta_c=\frac{N_i!}{\prod_{j=1}^Dx_{ij}!}\frac{\textrm{B}\left ( x_i+\alpha_c \right )}{\textrm{B}\left ( \alpha_c \right )} $

• multinoulli 모델의 한계를 극복
• 사전확률 줘서 관측 안된 단어 or 일부 단어에 대한 overfitting 방지를 해주는거라 볼 수 있음