1. Introduction
확률에 대한 두가지 관점
- 빈도론자(frequentist): 장기적인 관점에서 사건의 발생 빈도에 초점을 맞춤
- 베이지안(Bayesian): 확률은 불확실성을 정량화하기 위해 사용된다. 따라서 사건보다는 정보에 초점을 맞춘다.
- 장점: 사건에 대한 불확실성을 모델링하기 때문에 1. 관측이 적거나 2. 단기적으로 관측된 사건에 대해서 해석할 수 있다.
이 책에서는 베이지안 해석 관점을 채택함
다만, 확률론의 기본 원칙은 빈도론자나 베이지안 모두 동일하게 적용된다.
2. A brief review of probability theory
- $ p\left ( A \right ) $: 사건 A가 발생할 확률
- $ p\left ( \bar{A} \right ) $: 사건 A가 발생하지 않을 확률
2-1. 이진 확률 변수
이진 확률 변수(discrete random variable) X에 대해서..
$ p\left ( X=x \right ) = p\left ( x \right ) $
- $ p\left ( \cdot \right ) $: pmf(probability mass function)
- $ \sum_{x\in \mathfrak{X}}p\left ( x \right )=1 $
- 여기서 $ \mathfrak{X} $는 발생할 수 있는 모든 x 경우에 대한 set임
2-2. 근본 원칙
ㄱ. 두 사건의 합 (Probability of Union of two events)
- $ p\left ( A\cup B \right ) $ = $ p\left ( A \right ) + p\left ( B \right ) - p\left ( A\cap B \right ) $
- $ p\left ( A\cup B \right ) $ = $ p\left ( A \right ) + p\left ( B \right ) $ if A와 B가 상호배타적(mutual exclusive)일 때
- 참고> 상호배타적: 두 집합 A와 B 사이에 교집합이 없을 때
ㄴ. 결합확률 (joint probabilities)
- $ p\left ( A, B \right ) = p\left ( A\cap B \right )= p\left ( A|B \right )p\left ( B \right ) $: 결합확률을 product rule로 표현
- product rule은 chain rule로 표현될 수 있다.
- $ p\left ( X_{1:D} \right )=p\left ( X_{1} \right )p\left ( X_2|X_1 \right )p\left ( X_3|X_2,X_1 \right )\cdots p\left ( X_D|X_{1:D-1} \right ) $
- $ p\left ( A \right ) = \sum_{b}p\left ( A|B=b \right )p\left ( B=b \right ) $: marginal distribution (sum rule로 표현)
ㄷ. 조건부 확률 (Conditional probability)
- $ p\left ( A|B \right )=\frac{p\left ( A,B \right )}{p\left ( B \right )} $; $ p\left ( B \right ) $ > 0
2-3. 베이즈룰
베이즈룰 (Bates rule; Bayes Theory)
조건부 확률(Conditional probability)과 product & sum rules를 결합
- $ p\left ( X=x|Y=y \right ) = \frac{p\left ( X=x,Y=y \right )}{p\left ( Y=y \right )}=\frac{p\left ( X=x \right )p\left ( Y=y|X=x \right )}{\sum_{x'} p\left ( X={x}' \right )p\left ( Y=y|X=x' \right )} $
사용 예시
- 의료 진단
- 암에 걸렸을 때 (y=1), 진단 결과가 양성 (x=1)으로 나올 확률: $ p\left ( x=1|y=1 \right )=0.8 $
- 암에 걸릴 확률: $ p\left ( y=1 \right )=0.004 $
- 위양성 (암이 아닌데 진단 결과가 양성)일 확률: $ p\left ( x=1|y=0 \right )=0.1 $
- 진단 결과가 양성일 때 암일 확률: $ p\left ( y=1|x=1 \right )=\frac{p\left ( x=1|y=1 \right )p\left ( y=1 \right )}{p\left ( x=1|y=1 \right )p\left ( y=1 \right )+p\left ( x=1|y=0 \right )p\left ( y=0 \right )}=\frac{0.8\times 0.004}{0.8\times 0.004+0.1\times 0.996}=0.031 $
- 처음 $ p\left ( x=1|y=1 \right ) $ 에 비해서 실제로 양성 결과가 나왔을 때 암일 확률은 매우 낮다!
- 일반화된 분류기 (Generative classifiers)
- $ p\left (y=c|x,\theta \right )=\frac{p\left ( y=c|\theta \right )p\left ( x|y=c,\theta \right )}{\sum_{c'}p\left ( y=c'|\theta \right )p\left ( x|y=c',\theta \right )} $
- class의 조건부 분포와 class의 사전확을 통해 data의 class를 분류한다.
2-4.독립과 조건부 독립
독립(unconditionally independent / marginally independent)
- $ X\perp Y\Leftrightarrow p\left ( X,Y \right )=p\left ( X \right )p\left ( Y \right ) $
- 두 확률변수 X와 Y의 결합확률을 각 확률변수의 곱으로 표현할 수 있을 때 독립이라고 한다.
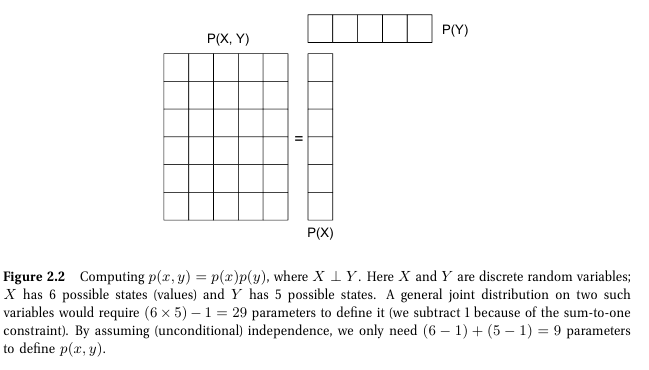
- 종속인 경우: 6 X 5 - 1개의 확률
- 독립인 경우: (6-1) + (5 -1)개 파라미터 필요 (각 경우에 대한 확률 곱이 결합확률로 나타남)
- 여기서 각 확률 변수의 합은 1이기 때문에 전체 경우의 수보다 1개 적은 파라미터 개수만 있으면 된다.
조건부 독립 (CI; Conditionally Independent)
- $ X\perp Y|Z \Leftrightarrow p\left ( X,Y|Z \right )=p\left ( X|Z \right )p\left ( Y|Z \right ) $
- 확률 변수 Z가 주어졌을 때, X와 Y가 Z에 대한 조건부 확률 곱으로 표현할 수 있을 때 조건부 독립이라고 한다.
- Theorem> 아래 function $ g $와 $ h $가 존재할 때 $X\perp Y|Z$이다.
- $ p\left ( x,y|z \right )=g\left ( x,z \right )h\left ( y,z \right ) $
- $ p\left ( z \right )>0 $
- 조건부 독립 가정 덕분에 소규모 데이터로 거대 확률 모델링을 할 수 있게 한다.
2-5. 연속 확률 변수
다음을 가정
- $ a\leq X\leq b $: 연속 확률 변수
- $ A=\left ( X\leq a \right ) $
- $ B = \left ( X\leq b \right ) $
- $ W = \left ( a\leq X\leq b \right ) $
- A와 W는 상호 배타적(mutually exclusive)
그럼 아래와 같은 식이 유추 가능
- $ B=A\vee W $
- $ p\left ( B \right )=p\left ( A \right )+p\left ( W \right ) $
- $ p\left ( W \right )=p\left ( B \right )-p\left ( A \right ) $
누적 분포 함수(cdf; cumulative distribution function)
- $ F\left ( q \right )\overset{\underset{\mathrm{def}}{}}{=}p\left ( X\leq q \right ) $
- 단조 증가 함수 (monotonically increasing function)다.
- 누적 분포함수를 통해 X의 확률을 다음과 같이 나타낼 수 있다.
- $ p\left ( a< X\leq b \right )=F\left ( b \right )-F\left ( a \right ) $
확률 밀도 함수(pdf; probability density function)
- $ f\left ( x \right )=\frac{d}{dx}F\left ( x \right ) $
- 확률 밀도 함수를 통해 X의 확률을 다음과 같이 나타낼 수 있다.
- $ P\left ( a< X\leq b \right )=\int_{a}^{b}f\left ( x \right )dx $
추가 내용
- $ P\left ( x\leq X\leq x+dx \right )\approx p\left ( x \right )dx $
- 충분히 작은 구간에 대해서는 $ p\left ( x \right )>1 $ 이 될 수 있다.
- 밀도의 합이 1이 되면 되기 때문
2-6. 퀀타일
F의 quantile
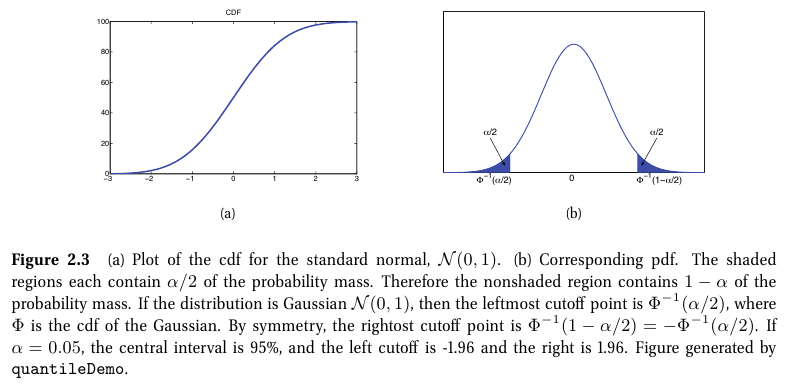
- F의 역함수
- $ F^{-1}\left ( \alpha \right )=P\left ( X\leq x_{\alpha } \right )=\alpha $
- cdf 기준으로 누적확률이 x, 그 누적확률이 나올 때의 위치가 y
2-7. 평균과 분산
평균($ \mu $; mean / expected value)
- $ \mathbb{E}[X]\overset{\underset{\mathrm{def}}{}}{=}\sum_{x\in \mathfrak{X}}xp\left ( x \right ) $: 이산 확률 변수에서 평균
- $ \mathbb{E}[X]\overset{\underset{\mathrm{def}}{}}{=}\int _{\mathfrak{X}}xp\left ( x \right )dx $: 연속 확률 변수에서 평균
분산($ \sigma ^2 $; variance)
- 분포의 퍼짐 정도
- $ var[X]\overset{\underset{\mathrm{def}}{}}{=}E[\left ( X-\mu \right )^2]=\int \left ( x-\mu \right )^2p\left ( x \right )dx=\int x^2p\left ( x \right )dx+\mu^2\int p\left ( x \right )dx-2\mu\int xp\left ( x \right )dx=\mathbb{E}[X^2]-\mu^2 $
- $ \mathbb{E}[X^2]=\mu^2+\sigma^2 $
표준 편차( $ \sigma $; standard deviation)
- $ std[X]\overset{\underset{\mathrm{def}}{}}{=}\sqrt{var[X]} $
3. Some common discrete distribution
3-1. 이산, 베르누이 분포
이산 분포 (binomial distribution)

- $ X\in \left\{0, ..., n \right\} $: 동전을 n번 던졌을 때 앞면이 나온 횟수
- $ \theta $: 동전이 앞면이 나올 확률
- $ X\sim Bin\left ( n , \theta \right ) $
- $ Bin\left ( k|n, \theta \right )\overset{\underset{\mathrm{def}}{}}{=}\binom{n}{k}\theta^k\left ( 1-\theta \right )^{n-k} $
- $ \binom{n}{k}\overset{\underset{\mathrm{def}}{}}{=}\frac{n!}{\left ( n-k \right )!k!} $
- 이산분포의 평균: $ n\theta $
- 이산분포의 분산: $ n\theta\left ( 1-\theta \right ) $
베르누이 분포 (Bernoulli distribution)
- $ X\in \left\{ 0, 1\right\} $: 동전을 한번 던졌을 때 앞면이 나온 횟수
- $ X \sim Ber\left ( \theta \right ) $
- $ Ber\left ( x|\theta \right )=\theta^{\mathbb{I}\left ( x=1 \right )}\left ( 1-\theta \right )^{\mathbb{I}\left ( x=0 \right )} $
- $ \theta $ if x = 1
- $ 1 - \theta $ if x = 0
3-2. 다항, 멀티 누이 분포
다항 분포(multinomial distribution)
- K-면체의 주사위를 n번 던졌을 때의 발생 확률
- $ \mathbf{x}=\left ( x_1, ..., x_K \right ) $: 벡터로, $ x_j $는 주사위에서 j면이 나온 횟수
- $ Mu\left ( \mathbf{x}|n,\theta \right )\overset{\underset{\mathrm{def}}{}}{=}\binom{n}{x_1...x_k}\prod_{j=1}^{K}\theta_j^{x_{j}} $
- $ \binom{n}{x_1...x_K}\overset{\underset{\mathrm{def}}{}}{=}\frac{n!}{x_1!x_2!\cdots x_K!} $
멀티 누이 분포(multinoulli distribution)
- K면체 주사위를 1번 던졌을 때 발생 확률
- $ \textbf{x}=[\mathbb{I}\left ( x=1 \right ),...,\mathbb{I}\left ( x=K \right )] $: dummy(one-hot) encoding
- $ Mu\left ( \mathbf{x} \right |1,\theta)=\prod_{j=1}^{K}\theta_j^{\mathbb{I}\left ( x_j=1 \right )} $
- $ Cat\left ( x|\theta \right )\overset{\underset{\mathrm{def}}{}}{=}Mu\left ( \textbf{x}|1,\theta \right ) $
- $ x \sim Cat\left ( \theta \right ) $이면, $ p\left ( x=j|\theta \right )=\theta_j $ 이다.
3-3. 포아송 분포
포아송 분포 (Poisson distribution)
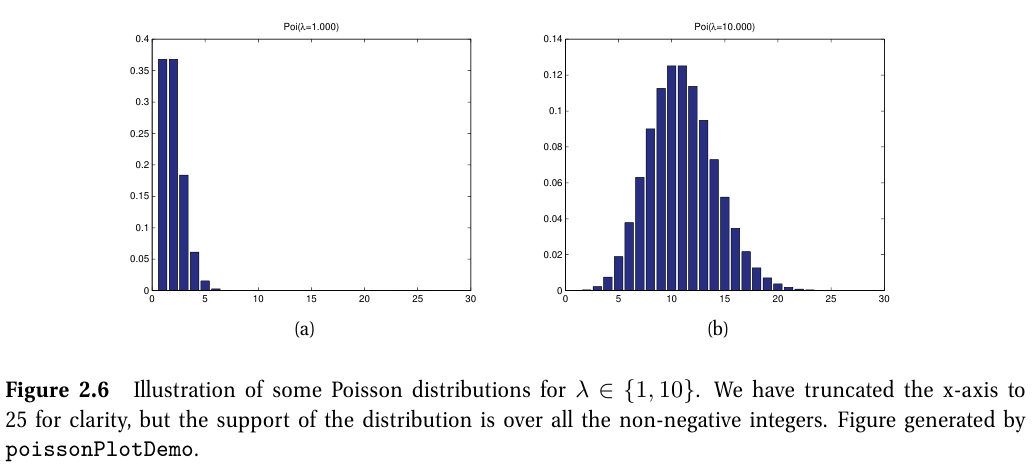
- 희귀하게 발생하는 사건들의 확률을 계산하기 위해 사용된다.
- use case
- 방사능 피폭 확률
- 교통 사고 확률
- $ X \sim \textrm{Poi}\left ( \lambda \right ) $
- $X\in \left\{ 0, 1, 2, ...\right\}$
- $ \lambda > 0 $
- $ \textrm{Poi}\left ( x|\lambda \right )=e^{-\lambda}\frac{\lambda^x}{x!} $
- $ e^{-\lambda} $: 정규화 상수로 분포의 합을 1로 보장
3-4. 경험 분포
경험 분포 (empirical distribution / empirical measure)
- $ \mathfrak{D}=\left\{ x_1,...,x_N\right\} $
- $ p_{emp}\left ( A \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{N}\sum_{i=1}^{N}\delta_{x_i}\left ( A \right ) $
- \delta_{x}\left ( A \right ): Dirac measure
- 0 if $ x\notin A $
- 1 if $ x \in A $
- 각 샘플별로 가중치(weight)를 부여할 수 있다.
- $ p\left ( x \right )=\sum_{i=1}^{N}w_i\delta_{x_i}\left ( x \right ) $
4. Some common continuous distribution
4-1. 정규 분포 (가우시안)
정규 분포 (normal /gaussian distribution)
$ \textit{N} \left ( x|\mu,\sigma^2 \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}\left ( x-\mu \right )^2} $
- $ \sqrt{2\pi \sigma ^{2}} $: 정규화 상수
- $ X \sim N\left ( 0, 1 \right ) $: 표준 정규 분포 (standard normal distribution)
- $ \lambda = \frac{1}{\sigma^2} $: precision
- high: 좁은 분포(분산 낮으며 평균 근처에 분포)
정규분포의 cdf
- $ \Phi \left ( x;\mu,\sigma^2 \right )\overset{\underset{\mathrm{def}}{}}{=}\int_{-\infty}^{x}N\left ( z|\mu,\sigma^2 \right )dz $
- cdf는 error function (erf) 관점에서 계산될 수 있다.
- $ \Phi \left ( x; \mu, \sigma \right )=\frac{1}{2}[1+erf\left ( z/\sqrt{2} \right )] $
- $ erf\left ( x \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^2}dt $
- 여기서 $ z=\frac{\left ( x-\mu \right )}{\sigma} $
통계에서 정규분포가 가장 많이 사용되는 이유
- 평균($\mu$)과 분산($\sigma^2$) 두 개의 파라미터만으로 분포의 특성을 표현할 수 있어 해석하기 쉽다.
- 중심 극한 정리(the central limit theorem)에 의해 독립 확률 변수들의 합은 가우시안 분포에 근사
- 가우시안 분포는 모델링할 때 필요한 가정이 적다.
- 데이터가 평균 주변에서 대칭적으로 분포
- 데이터 변동성이 분산으로 측정
- 수리적인 형식이 간단해 해석하기 쉽고 효율적임
4-2. 퇴화 분포 (degenerate pdf)
$ \displaystyle \lim_{\sigma^2 \to 0}N\left ( x|\mu, \sigma^2 \right )=\delta\left ( x-\mu \right ) $
- 정규 분포에서 $ \sigma ^2\to 0 $ 으로 갈 때, 분포는 평균 $ \mu $ 중심에서 매우 spike한 분포가 됨
Dirac delta function
$ \delta\left ( x \right ) $
- $ \infty $: x = 0
- $ 0 $: $ x\neq 0 $
- $ \int _{-\infty}^{\infty}\delta\left ( x \right )dx=1 $
델타 함수의 특성
- sifting property: 합이나 integral로 식을 빼낼 수 있다.
- $ \int^{\infty}_{-\infty}f\left ( x \right )\delta\left ( x-\mu \right )dx=f\left ( x \right ) $
정규 분포의 한계
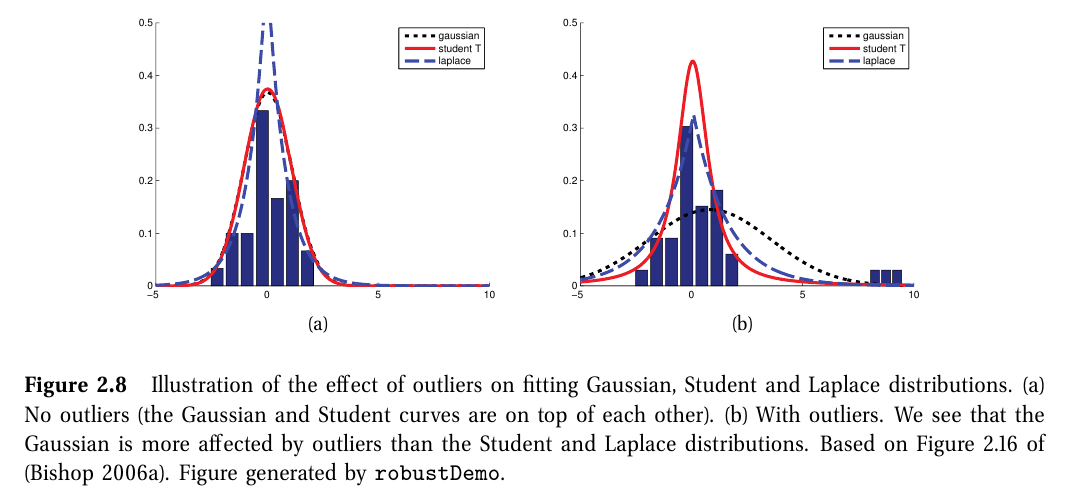
- 이상치(outlier)에 민감하다.
- 평균에서 멀어질수록 확률이 제곱승으로 크게 감소 -> 이상치에 대해서 잘 캐치할 수 없는 분포식
Student t 분포
$ T\left ( x|\mu,\sigma^2,v \right )\propto [1+\frac{1}{v}\left ( \frac{x-\mu}{\sigma} \right )^2]^{-\frac{v+1}{2}} $
- 정규분포에 비해 이상치에 강건하다.
- $ v > 0 $: 자유도 (degree of freedom)
- 보통 v=4를 일반적으로 사용함
- v >> 5 부터 가우시안 분포에 매우 근사하게 됨
- 평균과 중앙값은 같고, $ var=\frac{v\sigma^2}{\left ( v-2 \right )} $
- variance는 $ v > 2 $일 때만 정의 가능
- 평균은 $ v > 1 $일 때만 정의 가능
- variance 정의를 위해 보통 v > 2를 요구
4-3. 라플라스 분포
라플라스 분포(Lapalce distribution; double sided expotential distribution)
$ Lap\left ( x|\mu,b \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{2b}exp\left ( -\frac{|x-\mu|}{b} \right ) $
- 꼬리가 긴 분포 중 하나
- $ \mu $: location 변수
- $ b > 0 $: scale 변수
- $ \mu $: 평균, 중앙값
- $ 2b^2 $: 분산
라플라스 분포 특성
- 평균 근처에서 정규 분포보다 더 큰 확률 밀도를 가진다.
- 이상치에 대해서 정규분포보다 강건성을 가진다
-> 모델 sparisity를 보존하는데 유용한 특성

4-4. 감마 분포
감마 분포 (gamma distribution)

$ \textrm{Ga}\left ( T|shape=a, rate=b \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{b^a}{\Gamma \left ( a \right )}T^{a-1}e^{-Tb} $
- $ x > 0 $인 양수에 대한 확률 변수에 대한 유연한 분포
- shape ($ a > 0 $) 와 rate ($ b > 0 $) 두 개의 파라미터가 필요
- $ \Gamma\left ( x \right )\overset{\underset{\mathrm{def}}{}}{=}\int_{0}^{\infty}u^{x-1}e^{-u}du $: 감마함수
- $ \frac{a}{b} $: 평균
- $ \frac{a-1}{b} $: 중앙값
- $ \frac{a}{b^2} $: 분산
감마 분포의 특정 케이스들
- 지수 분포 (Exponential distribution)
- $ \textrm{Expon}\left ( x|\lambda \right )\overset{\underset{\mathrm{def}}{}}{=}Ga\left ( x|1,\lambda \right ) $
- 포아송 과정(Poisson process) 사건 간 시간을 나타내는 분포
- 사건은 독립적/연속적으로 단위시간동안 $ \lambda $만큼 발생한다.
- $ \lambda $: rate parameter
- 얼랑 분포 (Erlang distribution)
- $ \textrm{Erlang}\left ( x|\lambda \right )=Ga\left ( x|2, \lambda \right ) $
- 감마 분포에서 a가 양의 정수인 경우
- 보통 a = 2로 설정된다.
- $ \lambda $: rate parameter
- 카이스퀘어 분포 (Chi-squared distribution)
- $ \chi ^{2}\left ( x|\nu \right )\overset{\underset{\mathrm{def}}{}}{=}Ga\left ( x|\frac{\nu}{2},\frac{1}{2} \right ) $
- 가우시안 확률 변수들의 제곱 합에 대한 분포
- $ Z_{i}\sim N\left ( 0,1 \right ) $ 이고, $ S = \sum_{i=1}^{\nu}Z_i^2S = \sum_{i=1}^{\nu}Z_i^2 $ 이라 할 때, $ S\sim \chi_{nu}^2 $
- 역감마분포
- $ X \sim \textrm{Ga} \left ( a,b \right ) $라 할 때, $ \frac{1}{X} \sim \textrm{IG}\left ( a,b \right ) $이다.
- $ \textrm{IG}\left ( x|shape=a, scale = b \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{b^a}{\Gamma\left ( a \right )}x^{-\left ( a+1 \right )}e^{-\frac{b}{x}} $
- $ mean=\frac{b}{a-1}, mode=\frac{b}{a+1}, var=\frac{b^2}{\left ( a-1 \right )^2\left ( a-2 \right )} $
- 평균은 a>1일 때, 분산은 a >2일때 존재
4-5. 베타 분포
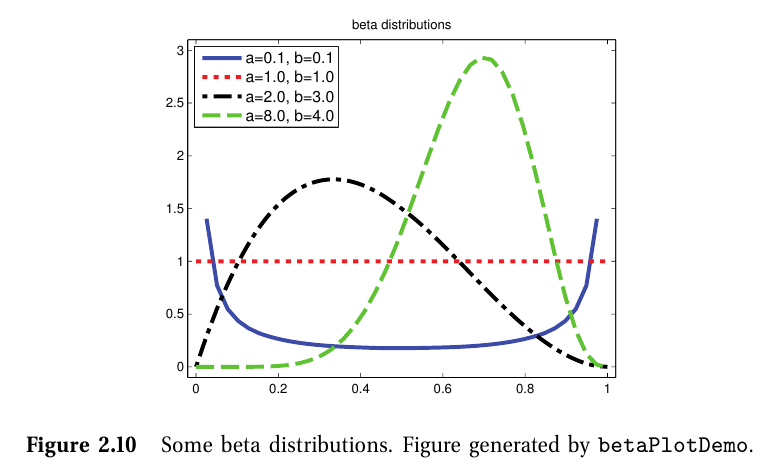
$ Beta\left ( x|a,b \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{B\left ( a,b \right )}x^{a-1}\left ( 1-x \right )^{b-1} $
- $ B\left ( a,b \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{\Gamma\left ( a \right )\Gamma\left ( b \right )}{\Gamma\left ( a+b \right )} $: beta function
- [0, 1] 구간에서 정의됨
- a, b > 0: 분포 합이 1이 되기 위한 조건
- a=b=1일 때 uniform 분포임
- a,b<1일 때, 0과 1부분에서 솟아오른 bimodal 분포임
- a,b>1일 때는 unimodal 분포임
- $ mean=\frac{a}{a+b},mode=\frac{a-1}{a+b-2},var=\frac{ab}{\left ( a+b \right )^2\left ( a+b+1 \right )} $
4-6. 파레토 분포
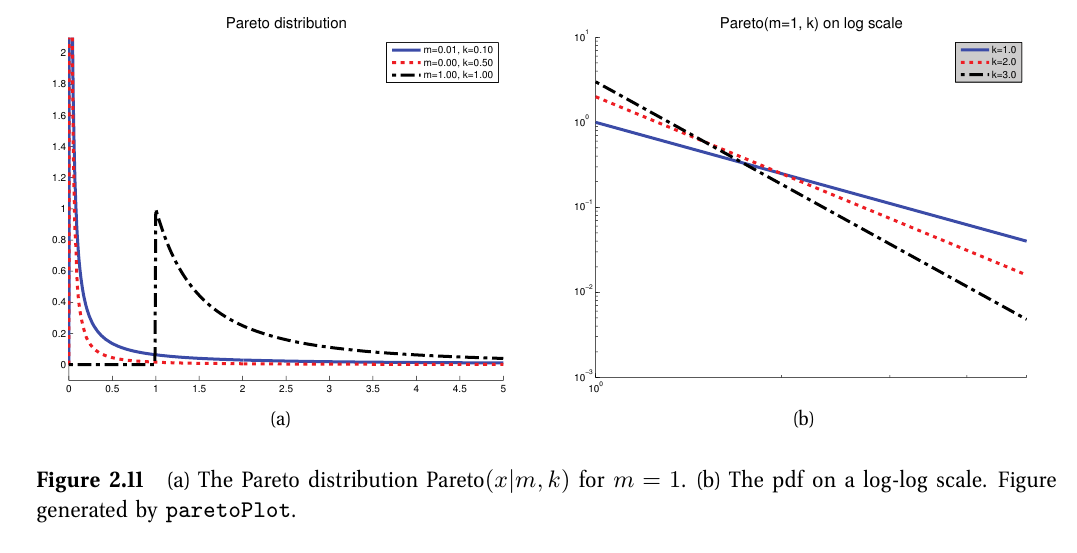
$ \textrm{pareto}\left ( x|k,m \right )\overset{\underset{\mathrm{def}}{}}{=}km^kx^{-\left ( K+1 \right )}\mathbb{I}\left ( x\geq m \right ) $
- 꼬리가 긴(long tails or heavy tails)인 분포를 모델링할 때 사용됨
- x는 상수 m보다 무조건 크며, k는 x가 m보다 얼마나 클지를 조절함
- $ k\to \infty $인 경우, 분포는 $\delta\left ( x-m \right )$에 근사한다.
- 분포를 log-log scale에 그리면 선형을 띈다.
- $ \textrm{log}p\left ( x \right )=a \textrm{log}x+c $
- $ mean=\frac{km}{k-1} $ if k > 1, $ mode=m $, $ var=\frac{m^2k}{\left ( k-1 \right )^2\left ( k-2 \right )} $ if k > 2
5. Joint probability distribution
결합 확률 분포
- $ p\left ( x_1, \cdots , x_D \right ) $, D > 1
- 변수간 관계에 대한 모델링 시 사용
- 모든 변수가 이산인 경우, 결합 분포를 다차원 행렬로 표현할 수 있고, 정의하는데 필요한 파라미터 수는 $ O\left ( K^D \right ) $이다.
- K는 각 변수의 상태 수
- 조건부 독립 가정을 통해서 고차원 결합 분포의 차원 수를 줄일 수 있다.
5-1. 공분산과 상관
공분산 (Covariance)
- $ Cov[X, Y]\overset{\underset{\mathrm{def}}{}}{=}\mathbb{E}[\left ( X-\mathbb{E}[X] \right )\left ( Y-\mathbb{E}[Y] \right )]=\mathbb{E}[XY]-\mathbb{E}[X]\mathbb{E}[Y] $
- 두 확률변수 X와 Y가 (선형적으로) 얼마나 연관이 있는지
- $ cov[X, Y]\propto [0,\infty) $
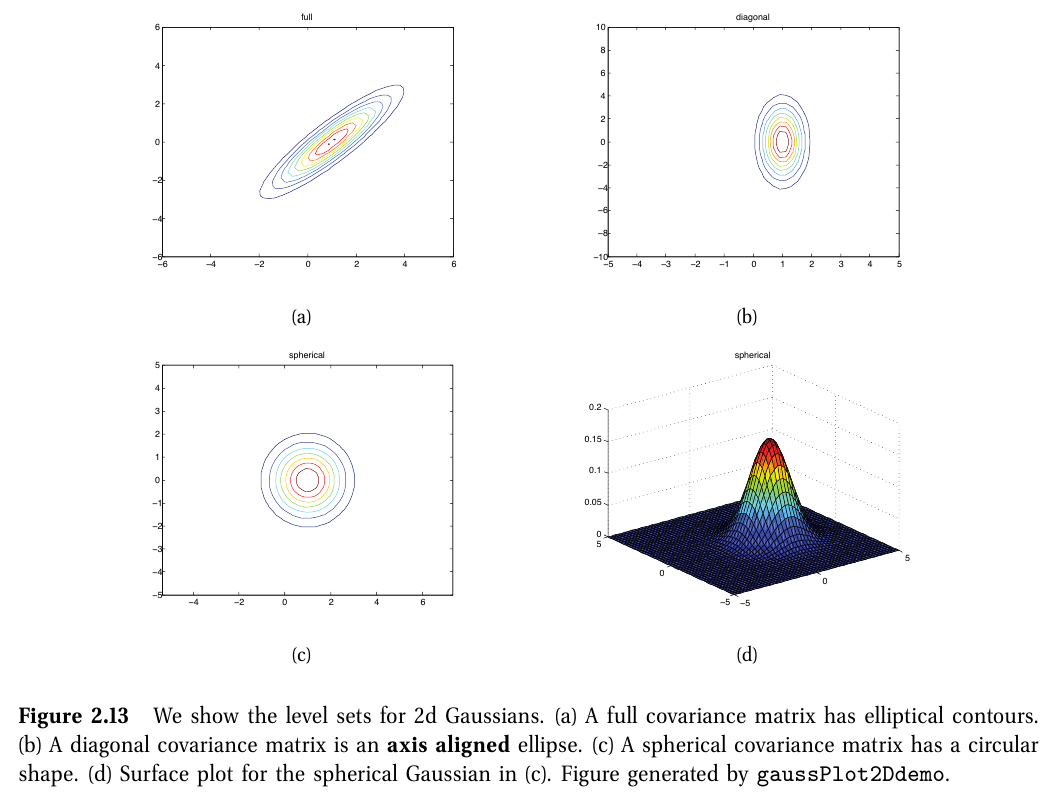
공분산 행렬 (covariance matrix)
- $ cov[x] \overset{\underset{\mathrm{def}}{}}{=} \mathbb{E}[\left ( x-\mathbb{E}[x] \right )\left ( x-\mathbb{E}[x] \right )^T] =$ \begin{pmatrix}
var[X_1] & cov[X_1,X_2] & \cdots & cov[X_1,X_d] \\
cov[X_2,X_1] & var[X_2] & \cdots & cov[X_2,X_d] \\
\vdots & \vdots & \ddots & \vdots \\
cov[X_d,X_1] & cov[X_d,X_2] & \cdots & var[X_d] \\
\end{pmatrix}
- x가 d-차원의 확률변수일 때, x의 covariance matrix는 대칭적, 양수로 정의된 행렬이다.
상관 계수 (correlation coefficient)

$ corr[X, Y]\overset{\underset{\mathrm{def}}{}}{=}\frac{cov[X,Y]}{\sqrt{var[X]var[Y]}} $
- 공분산을 정규화해 upper bound를 설정한 것
상관계수 행렬 (correlation matrix)
$ R=\begin{pmatrix}
corr[X_1,X_1] & corr[X_1,X_2] & \cdots & corr[X_1,X_d] \\
\vdots & \vdots & \ddots & \vdots \\
corr[X_d] & corr[X_d,X_2] & \cdots & corr[X_d,X_d] \\
\end{pmatrix} $
- $ -1\leq corr[X,Y]\leq 1 $
- 상관계수가 1인 경우
- 대각성분(diagonal elements)
- $ Y=aX+b $ 꼴로 완전 선형 관계를 가질 때
- 상관계수가 0인 경우
- $ X\perp Y\propto p\left ( X,Y \right )=p\left ( X \right )p\left ( Y \right ) $: 독립
- 단, 상관계수가 0인 것이 독립을 보장하진 않는다.
5-2. 다변량 가우시안
다변량 가우시안 (multivariate Gaussian or MVN; multivariate normal)
$ N\left ( x|\mu,\Sigma \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{\left ( 2\pi \right )^\frac{D}{2}|\Sigma|^{\frac{1}{2}}}exp[-\frac{1}{2}\left ( x-\mu \right )^T\Sigma^{-1}\left ( x-\mu \right )] $
- $ \mu=\mathbb{E}[x]\in \mathbb{R}^D $
- $ \Sigma=cov[x] \in R^{D\times D} $
5-3. 다변량 t-분포
다변량 t분포 (multivariate Student t distribution)
$ T\left ( x|\mu, \Sigma, \nu \right )=\frac{\Gamma\left ( \nu/2+D/2 \right )}{\Gamma\left ( \nu/2 \right )}\frac{|\Sigma|^{-1/2}}{\nu^{D/2}\pi^{D/2}}\times [1+\frac{1}{\nu}\left ( x-\mu \right )^T\Sigma^{-1}\left ( x-\mu \right )]^{-\frac{\nu+D}{2}} $
$ =\frac{\Gamma\left ( \nu/2 +D/2\right )}{\Gamma\left ( \nu/2 \right )}|\pi V|^{-1/2}\times[1+\left ( x-\mu \right )^TV^{-1}\left ( x-\mu \right )]^{-\frac{\nu+D}{2}} $
- MVN의 강건한 구조
- $ \Sigma $: scale 행렬
- $ V = \nu\Sigma $
- $ \nu $ 가 작을수록 꼬리가 두꺼워진다.
- $ \nu \to \infty $: Gaussian에 근사하게 된다.
- $ mean = mode = \mu, Cov = \frac{\nu}{\nu-2}\Sigma $
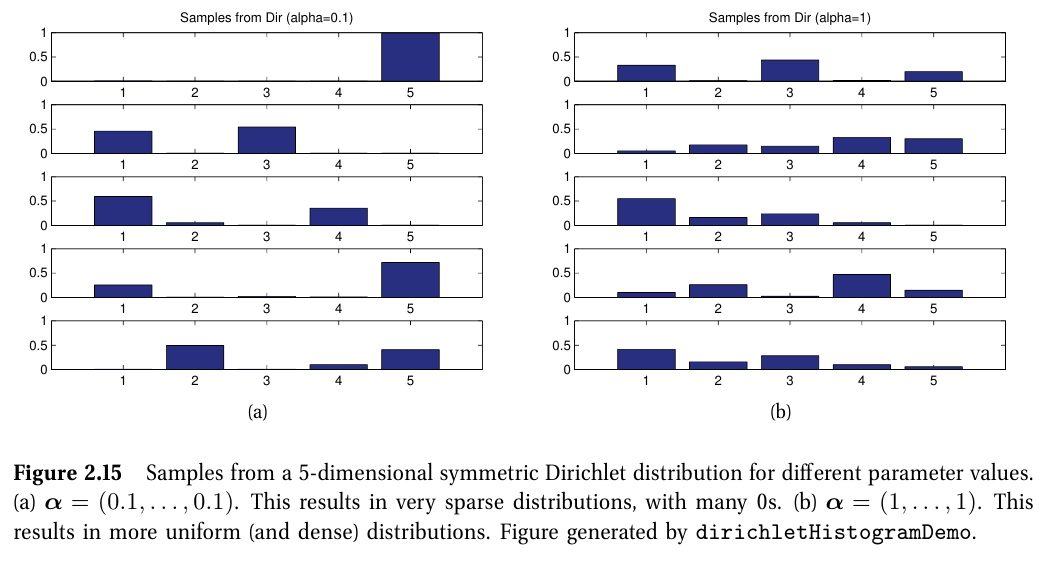
5-4. 디리클레 분포
디리클레 분포 (Dirichlet distribution)
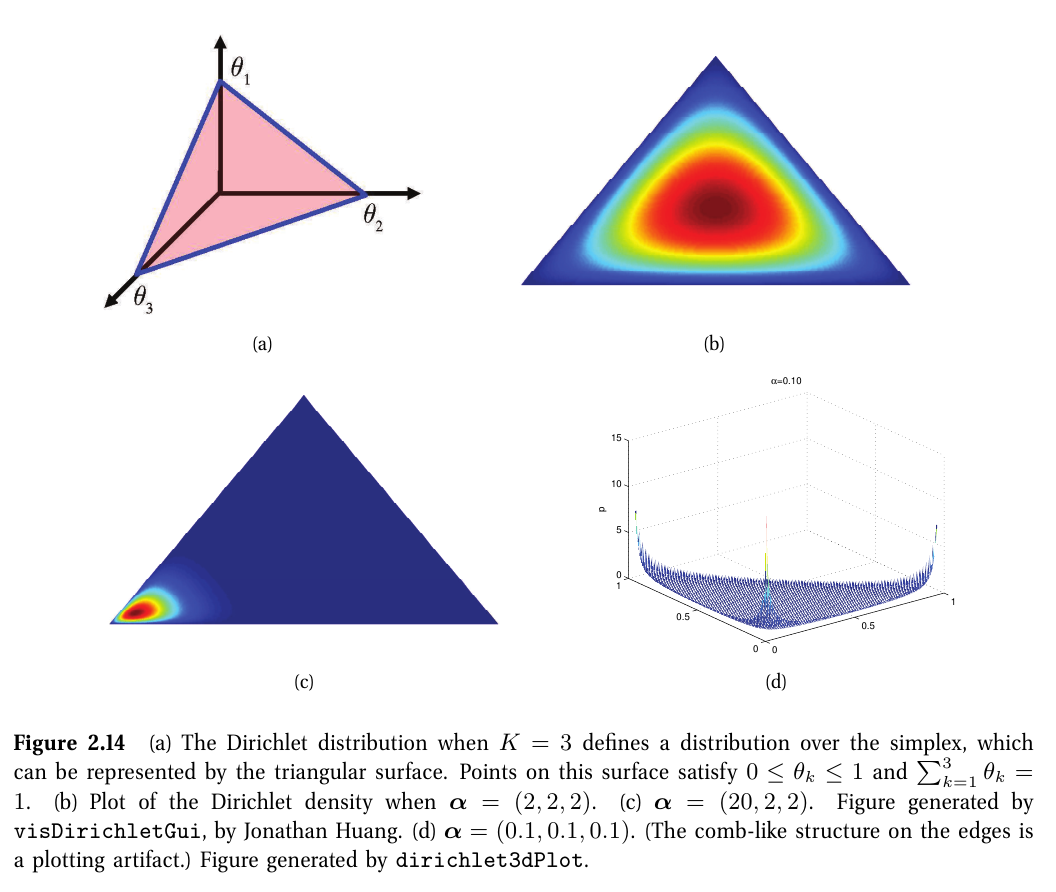
$ Dir\left ( x|\alpha \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{1}{B\left ( \alpha \right )}\prod_{k=1}^{K}x_k^{\alpha_k-1}\mathbb{I}\left ( x\in S_K \right ) $
- $ S_K=\left\{ x: 0 \leq x_k \leq 1, \sum_{k=1}^{K}x_k=1\right\} $
- 베타분포를 다변량일 때 일반화한 경우
$ B\left ( \boldsymbol{\alpha} \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{\prod_{k=1}^{K}\Gamma\left ( \alpha_k \right )}{\Gamma\left ( \alpha_0 \right )} $
- $ B\left ( \alpha_1, ..., \alpha_K \right ) $
- K개 변수가 있는 다변량일 때 베타함수를 일반화한 경우
- $ \alpha_0\overset{\underset{\mathrm{def}}{}}{=}\sum_{k=1}^{K}\alpha_k $: 분포의 peak 정도를 결정
- $ \alpha_k $: 어디서 peak가 될지 결정
- 모든 k에서 $ \alpha_k < 1 $이면, 주변부에서 확률이 치솟게 된다.
- $ \mathbb{E}[x_k]=\frac{\alpha_k}{\alpha_0},mode[x_k]=\frac{\alpha_k-1}{\alpha_0-K},var[x_k]=\frac{\alpha_k\left ( \alpha_0-\alpha_k \right )}{\alpha_0^2\left ( \alpha_0+1 \right )} $
6. Transformations of random variables
x ~ p()이고, y = f(x)일 때, y에 대한 분포가 어떻게 될지 알아보자!
6-1. 선형 변형
$ y=f\left ( x \right )=Ax+b $
- 여기서 f()는 선형 함수
$ \mathbb{E}[y]=\mathbb{E}[Ax+b]=A\mu+b $
$ \mathbb{E}[a^Tx+b]=a^T\mu+b $
$ cov[y]=cov[Ax+b]=A\Sigma A^T $
$ var[y]=var[a^Tx+b]=a^T\Sigma a $
6-2.일반 변형들
X가 이산 확률 변수 일 때
$ p_y\left ( y \right )=\sum_{x:f\left ( x \right )=y}p_x\left ( x \right ) $
X가 연속 확률 변수 일 때
$ P_y\left ( y \right )\overset{\underset{\mathrm{def}}{}}{=}P\left ( Y\leq y \right )=P\left ( f\left ( X \right ) \leq y\right )=P\left ( X\in \left\{ x|f\left ( x \right )\leq y\right\} \right ) $
$ P_y\left ( y \right )=P\left ( f\left ( X \right )\leq y \right )=P\left ( X\leq f^{-1}\left ( y \right ) \right )=P_x\left ( f^{-1}\left ( y \right ) \right ) $
여기서 cdf 미분을 통해 pdf를 구한다.
$ p_y\left ( y \right )\overset{\underset{\mathrm{def}}{}}{=}\frac{d}{dy}P_y\left ( y \right )=\frac{d}{dy}P_x\left ( f^{-1}\left ( y \right ) \right )=\frac{dx}{dy}\frac{d}{dx}P_x\left ( x \right )=\frac{dx}{dy}p_x\left ( x \right ) $
- $ x=f^{-1}\left ( y \right ) $
- $ dx $: x 공간의 measure of volume
- $ dy $: y 공간의 measure of volume
- $ \frac{dx}{dy} $: measure the change in volume
- 여기서 변화의 부호는 중요하지 않기 때문에 일반식을 얻기 위해서 절대값을 취해준다.
- $ p_y\left ( y \right )=p_x\left ( x \right )| \frac{dx}{dy} | $: change of variables formula
변수 다변량 변화 (multivariate change of variables)
자코비안 행렬 (J; Jacobian matrix)
$ J_{\textbf{x}\rightarrow \textbf{y}}\overset{\underset{\mathrm{def}}{}}{=}\frac{\partial \left ( y_1,\cdots ,y_n \right )}{\partial \left ( x_1,\cdots ,x_n \right )}\overset{\underset{\mathrm{def}}{}}{=}\begin{pmatrix}
\frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1 }{x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial y_n}{x_1} & \cdots & \frac{\partial y_n}{x_n} \\
\end{pmatrix} $
- y = f(x)
- $ |\mathrm{det}\textbf{J}| $: 함수 f를 적용 시, unit cube의 volume이 얼마나 변화하는지를 측정
여기서 f가 invertible mapping인 경우, 변수 y에 대한 pdf를 Jacobian을 통해 정의할 수 있다.
$ p_y\left ( \textbf{y} \right )=p\left ( \textbf{x} \right )|\textrm{det}\left ( \frac{\partial \textbf{x}}{\partial \textbf{y}} \right )|=p_x\left ( \textbf{x} \right )|\textrm{det} \textbf{J}_{\left ( \textbf{y}\to \textbf{x} \right )}| $
6-3. 중심 극한 정리

$ p\left ( S_N=s \right )=\frac{1}{\sqrt{2\pi N \sigma^2}}exp\left ( -\frac{\left ( s-N\mu \right )^2}{2N\sigma^2} \right ) $
- N이 증가할수록 확률변수들의 합은 정규분포에 근사한다.
- 여기서 $ S_N=\sum _{i=1}^NX_i $로 확률 변수들의 합
- 확률변수 $ p\left ( x_i \right ) $의 평균은 $ \mu $, 분산은 $ \sigma^2 $이며, 각각은 iid (independent and identically distributed).
중심 극한 정리 (the central limit theorem)
$ Z_N\overset{\underset{\mathrm{def}}{}}{=}\frac{S_N-N_{\mu} }{\sigma \sqrt{N}}=\frac{\bar{X}-\mu}{\sigma/\sqrt{N}} $
- 다음 양적 분포는 표준 정규 분포에 수렴한다.
- 여기서 $ \bar{X}=\frac{1}{N}\sum_{i=1}^{N}x_i $는 샘플 평균
7. Monte Carlo approximation
몬테 카를로 근사 (Monte Carlo approximation)

- 확률 변수의 분포 함수를 직접 구하는 것은 어려워 샘플로부터 근사해서 분포 함수를 구하는 방법
- 샘플 사이즈가 커질수록 MC 근사의 정확도는 상승한다.
- 방법
- 분포로부터 S개의 샘플 ($ x_1, \cdots x_S $)을 가져온다.
- 샘플들로부터 분포 f(x)를 근사한다. 근사는 $ \left\{ f\left ( x_s \right )\right\}_{s=1}^{S} $로 emprical distribution을 이용한다.
몬테 카를로 합 (Monte Carlo integration)
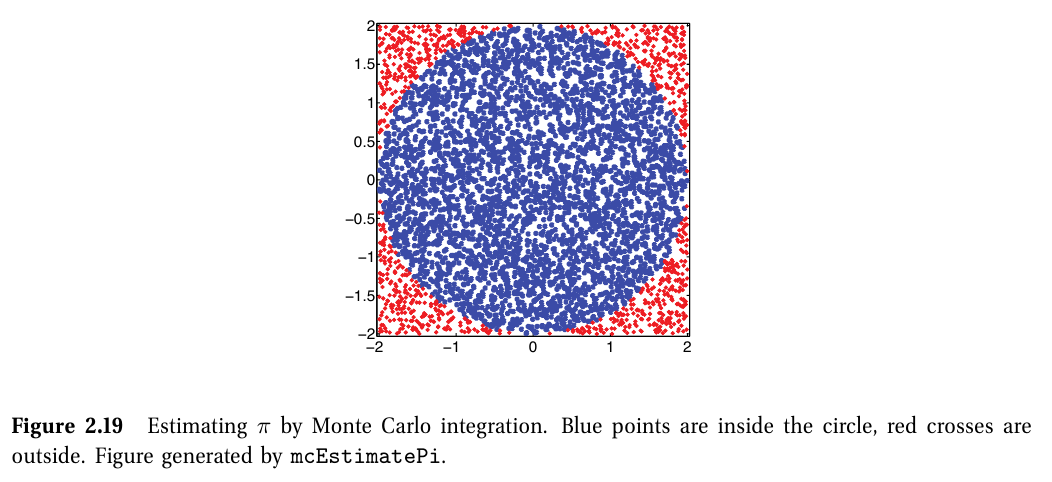
$ \mathbb{E}[f\left ( X \right )]=\int f\left ( x \right )p\left ( x \right )dx\approx \frac{1}{S}\sum_{s=1}^{S}f\left ( x_s \right ) $
- 샘플들은 확률적으로 무시할 수 없는 관측들로, 이 샘플들의 합을 통해 지표들이 계산된다.
유의미한 지표
- $ \bar{x}=\frac{1}{S}\sum _{s=1}^{S}x_{s}\to \mathbb{E}[X] $
- $ \frac{1}{S}\sum^S_{s=1}\left ( x_s-\bar{x} \right )^2\to \textrm{var}[X] $
- $ \frac{1}{S}\left\{ x_s\leq c\right\}\to P\left ( X\leq c \right ) $
- $ \textrm{median}\left\{ x_1,\cdots x_s\right\}\rightarrow \textrm{median}\left ( X \right ) $

8. Information Theory
8-1. 엔트로피
엔트로피 (entropy)
$ \mathbb{H}\left ( X \right )\overset{\underset{\mathrm{def}}{}}{=}-\sum_{k=1}^{K}p\left ( X=k \right )\textrm{log}_2p\left ( X=k \right ) $
- 확률 변수 X의 엔트로피는 해당 분포에 대한 불확실성을 수치화한 척도
- 위 정의는 K개 상태가 있는 이산 변수에 대한 엔트로피 정의임
- 최대 엔트로피 -> uniform distribution일 때
- 최소 엔트로피 -> 한가지 상태에 모든 확률이 있는 delta function일 때 (불확실성이 없음)
이진 확률 변수(binary random variable)일 때
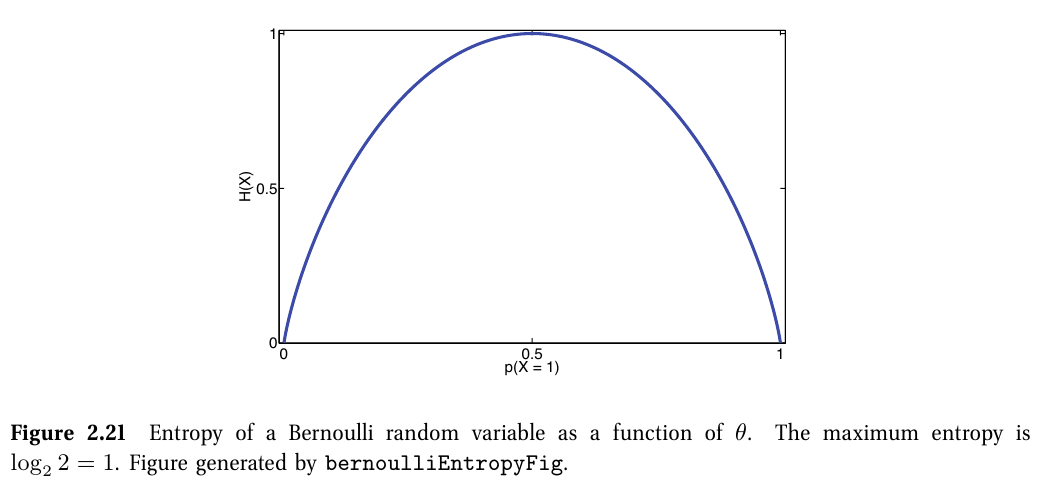
$ \mathbb{H}\left ( X \right )=-[p\left ( X=1 \right )\textrm{log}_2p\left ( X=1 \right )+p\left ( X=0 \right )\textrm{log}_2p\left ( X=0 \right )]=-[\theta\textrm{log}_2\theta+\left ( 1-\theta \right )\textrm{log}_2\left ( 1-\theta \right )] $
8-2. 쿨백 라이블러 발산
쿨백 라이블러 발산 (KL divergence; Kullback-Leibler divergence)
$ \mathbb{KL}\left ( p||q \right )\overset{\underset{\mathrm{def}}{}}{=}\sum_{k=1}^{K}p_k\textrm{log}\frac{p_k}{q_k} $
- 두 확률 분포 p와 q의 차이점(dissimilarity)을 측정하는 지표
- p를 잘 모를 때 q를 통해서 p를 근사 시 남아있는 불확실성을 나타냄
$ \mathbb{KL}\left ( p||q \right )=\sum_{k}p_k\textrm{log}p_k-\sum _kp_k\textrm{log}q_k=-\mathbb{H}\left ( p \right )+\mathbb{H}\left ( p,q \right ) $
- $ \mathbb{H}\left ( p,q \right )\overset{\underset{\mathrm{def}}{}}{=}-\sum _kp_k\textrm{log}q_k $: cross entropy
- 모델 q를 코드북으로 정의할 때, 분포 p로부터 나오는 데이터를 인코딩하는데 필요한 평균 비트 수
- 이를 통해 KL divergence는 데이터 인코딩에 필요한 추가 비트 평균 수로 볼 수 있음
- 이는 실제 분포 p에 대해서 분포 q를 인코딩에 사용하기 때문임.
- 따라서 $ \mathbb{KL}\left ( p||q \right )\geq 0 $이고, q=p일 때 KL은 0이다.
[Theorem] $ \mathbb{KL}\left ( p||q \right )\geq 0 $ with equality iff p = q (Information inequality)
(증명) Jensen's inequality를 사용해 증명
8-3. 상호정보
상호 정보(MI; Mutual Information)
$ \mathbb{I}\left ( X;Y \right )\overset{\underset{\mathrm{def}}{}}{=}\mathbb{KL}\left ( p\left ( X,Y \right )||p\left ( X \right )p\left ( Y \right ) \right )=\sum _x\sum_yp\left ( x,y \right )\textrm{log}\frac{p\left ( x,y \right )}{p\left ( x \right )p\left ( y \right )} $
- 결합 분포 $ p\left ( X, Y \right ) $가 두 분포의 곱 $ p\left ( X \right )p\left ( Y \right ) $과 얼마나 유사한지 측정하는 지표
- $ \mathbb{I}\left ( X;Y \right )\geq 0 $ with equality iff $ p\left ( X,Y \right )=p\left ( X \right )p\left ( Y \right ) $ (독립일 때 MI는 0)
$ \mathbb{I}\left ( X;Y \right )=\mathbb{H}\left ( X \right )-\mathbb{H}\left ( X|Y \right )=\mathbb{H}\left ( Y \right )-\mathbb{H}\left ( Y|X \right ) $
- $ \mathbb{H}\left ( Y|X \right )=\sum_{x}p\left ( x \right )\mathbb{H}\left ( Y|X=x \right ) $: conditional entropy
- Y를 관측했을 때 X에 대한 불확실성 감소 정도 또는 X를 관측했을 때 Y에 대한 불확실성 감소 정도로 MI를 해석할 수 있다.
점별 상호 정보량 (PMI; pointwise mutual information)
$ \textrm{PMI}\left ( x,y \right )\overset{\underset{\mathrm{def}}{}}{=}\textrm{log}\frac{p\left ( x,y \right )}{p\left ( x \right )p\left ( y \right )}=\textrm{log}\frac{p\left ( x|y \right )}{p\left ( x \right )}=\textrm{log}\frac{p\left ( y|x \right )}{p\left ( y \right )} $
- 사건들이 우연히 일어날 기댓값에 비해 함께 일어나는 불일치 정도를 척도화한 것
- X와 Y의 MI는 PMI의 기댓값이다.
연속 확률변수에서의 상호 정보량
- 연속 확률 변수를 이산화하거나 정량화하여서 계산할 수 있다.
- bin(간격)의 크기나 위치에 따라서 결과가 달라질 수 있다.
'Study > 머신러닝' 카테고리의 다른 글
| [머피 머신러닝] Chapter 3. Generative models for discrete data (0) | 2025.02.04 |
|---|---|
| [머피 머신러닝] Chapter 1. Introduction (0) | 2025.01.22 |