1장. 알고리즘 기초
요약
책에서 앞으로 공부할 각 단원의 내용마다 왜 공부해야하는지, 어떤 내용이 있는지 핵심요소들을 거시적으로 정리하는 장이었다.
내용 정리
1.1 알고리즘 정의하기
- 알고리즘(Algorithm): 문제를 풀기 위해 특정한 연산을 수행하는 규칙
- 정해진 포맷의 입력 데이터를 정의된 연산 규칙에 따라 처리해서 결과를 출력한다.
- 알고리즘을 설계하는 것은 가장 효율적인 방법으로 현실의 문제를 해결하는 과정이다.
- 기본적인 알고리즘들의 조합은 더 큰 범위의 문제를 해결하는데 적용될 수 있다.
- 알고리즘의 개발, 배포, 사용 단계
- 문제 정의
- 알고리즘 설계
- 알고리즘 구현
- 알고리즘 검증
- 배포 및 사용
- 개발 단계: 설계 단계 + 구현 단계
- 개발 단계에서 설계와 구현 과정을 반복하면서 효율적인 알고리즘을 찾아나가게 됨
- 설계 단계: 알고리즘 구조와 작동 방식, 구현 방법을 결정하고 문서화
- 정확도와 성능을 모두 고려해야 함
- 사용될 수 있는 여러 알고리즘 후보군들을 추리고 특징, 장단점을 비교하는 과정을 반복함
- 문제가 복잡할수록 효율적 알고리즘을 결정하는 설계 단계가 중요함
- 구현 단계: 설계한 알고리즘을 컴퓨터 프로그램으로 구현하는 단계
- 설계 단계에서 정의한 작동 방식과 구조를 정확하게 구현하는 것이 중요함
- 개발 단계에서 기능적/비기능적 요구사항을 만족시키는 설계도를 작성함
- 모든 요구사항을 충족하는 설계도를 작성하기 위해 많은 시간과 노력을 들일 필요가 있음
- 기능적 요구사항: 데이터가 주어졌을 때 어떻게 출력될지 결정하는 것
- 비기능적 요구사항: 입력 데이터를 처리하는데 걸리는 시간/공간 등 성능과 관련됨
- 알고리즘 검증은 개발된 알고리즘이 요구사항들을 잘 만족하는지 점검한다.
- 기능적 알고리즘 검증: 정해진 포맷의 결과가 출력되는지
- 비기능적 알고리즘 검증: 정해진 제약조건 안에서 주어진 성능을 만족하는지
- 알고리즘 배포: 해당 코드가 실행될 실제 환경에 대한 설계를 수반
- 프로덕션 환경을 구성하여 테스트함
- 프로덕션 환경: 실제로 알고리즘이 처리할 데이터와 프로세싱이 구동될 환경과 유사하게 구현
1.2 알고리즘의 로직 표현하기
- 알고리즘 설계 시 가능한 여러 방법을 탐색하는 것이 중요함
- 특히 알고리즘의 작동 방식과 구조를 적절히 표현할 수 있는 능력이 필요함
- 이유: 알고리즘 구현 방법을 남들과 공유하거나 설명하기 위해서
- 의사코드(pseudocode): 알고리즘 작동 방식을 표현하는 가장 단순한 방법으로 알고리즘의 특징들을 코드 형식으로 구조화해 기술한 것
- 적절히 작성된 의사코드를 통해 알고리즘의 핵심 흐름들을 이해할 수 있다.

- 스니펫(snippet): 알고리즘의 핵심 구현 원리를 프로그래밍 언어 코드로 나타낸 것
- 최근 알고리즘 논리를 의사코드 대신 파이썬 등 가독성 좋은 프로그래밍 코드들로 직접 표현하는 경우가 늘고 있다.
- 장점
- 지나치게 상세한 논리 기술은 피하면서 알고리즘의 중요 논리와 구조는 표현할 수 있다는 장점이 있다.
- 의사코드 기술하는 단계를 생략할 수 있다.
- 단점
- 모든 의사코드를 스니펫으로 대체하긴 어렵다. 특히 스니펫에 불필요한 코드나열은 의사코드를 이용해 한줄로 추상화하는게 가독성이 좋을 수 있다.
- 실행 계획(execution plan): 하나의 알고리즘을 주요 작업(task)으로 분리해 표현하는 것
- 장점
- 알고리즘의 작동 원리가 복잡한 경우는 간단한 그림으로 표현하는 것이 이해하기 쉽다.
- 단점
- 세부 구현방식은 알기 어렵다.
- 장점

1.3 파이썬 패키지 살펴보기
파이썬은 공식 홈페이지 (https://www.python.org) 에서 다운받을 수 있다.
최근에는 파이썬 관련 여러 유용한 툴을 묶어놓은 아나콘다(Anaconda)도 많이 사용한다. 공식 홈페이지는 https://continuum.io/downloads 이다.
- 파이썬에서 사용할 외부 라이브러리 설치 방법
- 설치하는 여러 방법이 있으며, 그 중 pip와 conda를 이용해 설치하는 방법을 소개한다.
- 명령 셸의 CLI 환경에서 아래 pip 명령어를 통해 외부 라이브러리를 설치/업그레이드 할 수 있다.
- conda로 설치하는 방식은 pip와 동일하다.
## pip를 이용한 방법
pip install <패키지 이름> # 패키지 설치
pip install <패키지 이름> --upgrade # 패키지 최신버전 업그레이드
## conda를 이용한 방법
conda install <패키지 이름> # 패키지 설치
conda upgrade <패키지 이름> # 패키지 최신버전 업그레이드
최근 파이썬으로 머신러닝, 딥러닝 등의 연구가 이루어지면서 이와 관련된 함수를 제공하는 여러 라이브러리들이 생기고 있다.
- Scipy: 수학, 과학 관련 함수들을 제공하는 라이브러리 묶음으로 목록은 아래와 같다.
- Numpy: 행렬, 배열 등 연산 지원
- Scikit-learn: 머신러닝 알고리즘 제공
- pandas: 테이블형 자료구조를 제공
- Matplotlib: 시각화 패키지
- Seaborn: Matplotlib보다 방식이 간단한 시각화 패키지
- iPython: 파이썬 코드를 대화형으로 작성하는 콘솔
주피터 노트북을 이용하면 코드들을 shell 단위로 실행할 수 있어 결과를 빠르게 확인할 수 있다.
1.4 알고리즘 설계 기법 이해하기
알고리즘 설계 시 고려 사항
- 기대한 결과가 출력되는가?
- 알고리즘이 효율적인가?
- 지금보다 더 큰 데이터셋에서도 동작하는가?
여기서 중요한 것은 문제가 얼마나 복잡한지 이해하는 것이다.
문제의 복잡도를 이해하려면 문제의 특성에 따라 설계할 알고리즘 유형을 알아야 한다.
또한 문제를 데이터 차원, 연산 차원으로 풀이할 수 있어야 한다.
- 알고리즘 유형
- 데이터 집약적 알고리즘: 대규모 데이터 처리를 위해 설계된 알고리즘이나 알고리즘 원리는 상대적 단순한 경우
- 연산 집약적 알고리즘: 높은 연산 수준을 요구하지만 데이터는 크지 않은 경우
- 병렬화는 연산 집약적 알고리즘의 성능을 극대화할 수 있다.
- 데이터/연산 집약적 알고리즘: 대규모 데이터에 대해 높은 연산을 해야하는 경우
- 자원 소모가 많기 때문에 신중히 설계해야하며, 가능한 자원을 지능적으로 할당해야 한다.
- 데이터 차원 (3V): 데이터 차원별 유형을 이해하고, 효과적으로 저장, 처리할 수 있는 알고리즘 설계가 필요하다.
- 크기(Volume): 알고리즘이 처리할 것으로 예상되는 데이터 크기
- 속도(Velocity): 새로운 데이터가 생성되는 속도. 속도는 0일 수 있다.
- 다양성(Varity): 알고리즘이 처리할 것으로 예상되는 데이터 유형의 수
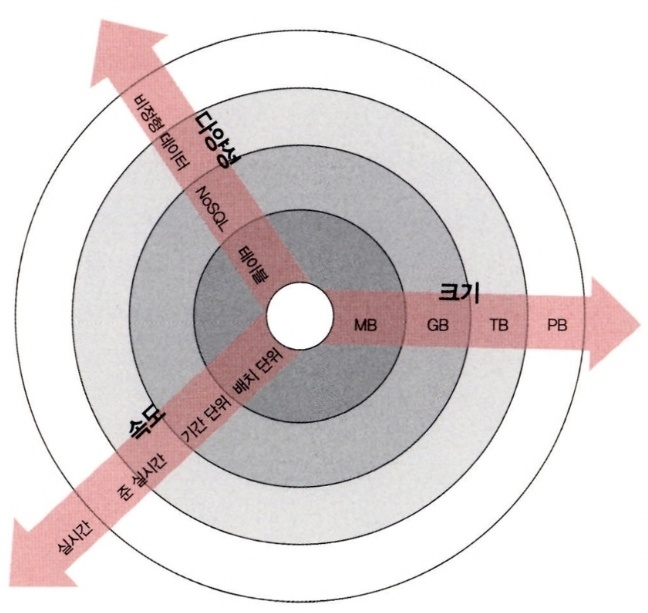
- 연산 차원: 문제를 처리하는데 소요되는 컴퓨팅 자원에 적절하게 연산처리를 할 수 있어야 한다.
- 알고리즘 프로세싱이 어떤 것을 요구하는지 판단하여 적절한 연산을 선택해야 한다.
- 가용 가능한 리소스 크기를 이해하고 알고리즘을 설계할 수 있어야 한다.
1.5 성능 분석
- 알고리즘 설계시 필수 사항
- 알고리즘은 설계 의도에 맞게 정확해야 한다.
- 알고리즘 구현 방식을 이해할 수 있어야 한다.
- 알고리즘은 효율적이어야 한다.
여기서 효율성은 알고리즘의 성능과 크게 연결된다. 따라서 알고리즘의 성능 분석이 중요하다.
- 알고리즘 성능 분석은 설계 단계에서 가장 중요한 단계
- 성능 측정 방법: 알고리즘의 복잡성을 파악
- 복잡성 파악은 보통 복잡도 분석을 통해 이루어진다.
- 복잡도 이론: 알고리즘이 얼마나 복잡한지 판단하는 도구
- 알고리즘 복잡도 분석 방법
- 공간 복잡도 분석
- 시간 복잡도 분석
- 공간 복잡도 분석(Space complexity analysis): 알고리즘이 입력 데이터를 처리하는데 필요한 메모리 양을 추정
- 알고리즘이 처리되는데 필요한 하드웨어 메모리 사양을 분석
- 알고리즘의 효율적 설계를 위해서 필수적이다.
- 공간 복잡도 분석이 제대로 수행되지 않으면 데이터를 저장할 메모리가 부족한 현상이 발생해 알고리즘 성능과 효율성에 악영향을 줄 수 있다.
- 최근에 분산 컴퓨팅 기술이 도입되면서 처리해야 할 데이터양이 커짐에 따라 공간복잡도 분석이 중요해지고 있다.
- 시간 복잡도 분석 (Time complexity analysis): 알고리즘에 할당한 작업을 완료하는데 걸리는 시간을 추정
- 알고리즘 자체 구조에 영향을 받게 된다.
- 시간 복잡도 분석을 통해 알고리즘의 확장 가능성, 더 큰 데이터셋을 다루는데 적절한지 여부 등을 판단할 수 있다.
- 시간 복잡도 분석을 통해 문제를 풀 수 있는 알고리즘들중 가장 효율적인 알고리즘을 찾아낼 수 있다.
- 시간 복잡도 계산 방법
- 구현 후 프로파일링 분석 방식: 구현 후 실행 시간을 비교
- 구현 전 이론적 분석 방식: 성능을 수학적으로 근사해 비교
- 이론적 분석 방식은 알고리즘 구조 자체에만 집중할 수 있다는 장점이 있다.
입력한 데이터는 여러가지 특성이 있을 수 있다 (정렬이 되었거나, 무작위이거나 등). 따라서 알고리즘 성능 추정 시에는 최상, 최악, 평균의 경우를 고려해야 한다.
- 최상의 경우: 알고리즘이 최고의 성능을 낼 수 있도록 입력 데이터가 정리된 경우
- 성능의 상한선을 확인할 수 있다.
- 최악의 경우: 작업을 완료하는데 걸리는 시간이 최대인 경우로 데이터가 정리된 경우
- 성능의 하한선을 확인할 수 있다.
- 대규모 데이터를 가진 복잡한 문제에 대한 알고리즘 성능을 측정할 때 유용하다.
- 평균의 경우: 여러 입력 데이터들의 성능을 분석할 때 이들의 평균 결과
- 성능의 평균을 확인할 수 있다.
- 단점: 항상 정확하진 않고 여러 데이터에 대한 성능 평가가 필요하기 때문에 실행이 어렵다.
시간 복잡도는 보통 빅오 표기법으로 표현되며, 이를 통해 가장 빠른 알고리즘이 무엇인지 유추할 수 있다.
- 빅오 표기법(Big O notation): 최악의 경우 시간복잡도를 입력 데이터 크기로 나타내는 표기방법
- 보통 O와 입력 데이터 크기 n을 이용해서 이론적인 시간복잡도를 표기한다.
- 상수 시간 복잡도: 입력 데이터의 크기에 상관없이 항상 알고리즘 실행 시간이 일정할 때
- 표기법: O(1)
## 상수 시간 복잡도 함수의 예
# getFirst: 리스트의 첫번째 원소를 반환하는 함수
def getFirst(myList):
return myList[0]
# ex 1)
getFirst([1, 2, 3])
>> 1
# ex 2)
getFirst([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
>> 1
배열의 크기에 상관없이 항상 첫번째 원소만을 가져옴으로 time complexity는 O(1)이다.
다음 알고리즘들도 상수 시간 복잡도 O(1)을 가진다.
- 예시 1: 스택에 push/pop으로 요소를 추가/제거할 때
- 예시 2: 해시 테이블에 담긴 요소에 접근할 때
- 선형 시간 복잡도: 알고리즘 실행 시간이 입력 데이터의 크기 (n) 에 비례할 때
- 표기법: O(n)
## 선형 시간 복잡도 함수의 예
# getSum: 각 list의 값들을 하나씩 가져와서 sum 변수에 더한 후 최종 값을 출력하는 함수
def getSum(myList):
sum = 0
for item in myList:
sum += item
return sum
# 예시 1
getSum([1, 2, 3])
>> 6
# 예시 2
getSum([1, 2, 3, 4])
>> 10배열의 크기에 따라 선형적으로 알고리즘 연산 시간이 늘어나기 때문에 time complexity는 O(n)이다.
다음 알고리즘들도 선형 시간 복잡도 O(n)을 가진다.
- 예시 1: 1차원 배열에서 값이 있는 위치를 검색하는 작업
- 예시 2: 1차원 배열에서 가장 작은 값을 찾아내는 작업
- 이차 시간 복잡도: 입력 데이터 크기 제곱에 비례해서 실행 시간이 증가하는 알고리즘
- 표기법: O(n^2)
## 이차 시간 복잡도 함수의 예
# getSum2: 이차원 배열에 담긴 각 요소들의 값을 sum 값에 더하여서 최종 sum을 출력하는 함수
def getSum2(myList):
sum = 0
for row in myList:
for item in row:
sum += item
return sum
# 예시 1
getSum([[1, 2],
[3, 4]])
>> 10
# 예시 2
getSum([[1, 2, 3],
[4, 5, 6]])
>> 21배열의 크기의 제곱만큼 알고리즘 연산 시간이 늘어나기 때문에 time complexity는 O(n^2)이다.
다음 알고리즘들도 이차 시간 복잡도 O(n^2)을 가진다.
- 예시 1:버블 정렬(bubble sort) 알고리즘
- 로그 시간 복잡도: 입력 데이터 크기에 로그값을 취한 크기에 비례해서 실행 시간이 증가하는 알고리즘
- 표기법: O(log(n))
- 루프를 순회할 때마다 입력 데이터 크기는 일정 배수로 줄어듦
## 로그 선형 시간복잡도 함수의 예
# searchBinary: 바이너리 서치를 구현한 함수.
def searchBinary(myList, item):
first = 0
last = len(myList) - 1
foundFlag = False
while (first <= last and not foundFlag):
mid = (first + last) // 2
if myList[mid] == item:
foundFlag = True
else:
if item < myList[mid]:
last = mid - 1
else:
first = mid + 1
return foundFlag
# 예시 1
searchBinary([8, 9, 10, 100, 1000, 2000, 3000], 10)
>> True
# 예시 2
searchBinary([8, 9, 10, 100, 1000, 2000, 3000], 5)
>> False탐색 시마다 이전 크기의 절반으로 줄어들면서 탐색하기 때문에 O(log(n)) 시간복잡도를 가짐
또한 리스트는 미리 정렬이 되어 있어야 한다.
- 입력 데이터 크기에 비례해서 실행 시간이 증가하는 유형
- 최악의 성능: O(n^2)
- 최고의 성능: O(log(n))
- O(log(n))을 항상 달성할 수 있는 것이 아니지만 모든 알고리즘 성능의 기준이다.
- 근사 알고리즘(approximate algorithm): 알고리즘의 정확도를 희생하더라도 복잡도를 줄이는 방법
1.6 알고리즘 검증
알고리즘 검증을 통해 가능한 많은 입력 케이스들의 결과가 정상적으로 출력되는지 확인해야 한다.
이 때 유효성 검사를 통해 알고리즘이 적절한 해결책인지 확인할 수 있다.
검증 방법은 알고리즘의 종류에 따라 달라진다.
- 결정론 관점에서의 알고리즘의 종류
- 결정론적 알고리즘: 같은 입력 값에 대해 언제나 동일한 결과를 출력한다.
- 비결정론적 알고리즘: 난수 값에 따라 입력 데이터의 결과가 달라지게 된다.
- 속도 관점에서의 알고리즘 종류
- 최적(exact) 알고리즘: 문제에 대한 정확한 해결책을 찾아내는 알고리즘
- 근사(approximate) 알고리즘: 문제가 복잡한 경우 몇가지 가정을 통해 문제를 단순화해서 푸는 알고리즘
- 문제에 대한 최적의 해결책을 제공하지는 않는다.
- 문제의 요구사항을 파악할 때 정확도에 대한 기대치를 설정하는것
- 근사 알고리즘은 결과가 허용가능 범위 내에 위치하는지에 따라서 유효성을 판단하게 된다.
- ex> 외판원 문제
중요한 의사결정을 해야되는 문제에서 알고리즘이 사용된다면 알고리즘이 출력한 결과를 해석할 수 있어야 한다.
알고리즘을 통해 얻은 결과가 편향된 것인지 판단할 수 있어야 하기 때문이다.
- 해석 가능성(explainability): 결론을 내리는데 어떤 변수들이 얼마나 영향을 미치는지 판단하는 능력
- 알고리즘이 도출한 결론이 파급력 있는 영향력을 행사할 때는 알고리즘이 가진 편향과 편견을 면밀히 검증해야 한다.
- 특히 사람들의 안전, 윤리와 관련되어 있을 때는 해석 가능성이 중요하게 된다.
- 해석 가능성에 모델 무관 국소적 해석 기법(LIME) 등의 기법이 사용된다.
참고
학습 Point !
- 알고리즘의 로직은 이전에 의사코드(pseudocode)로 작성되었지만 최근에는 파이썬 코드가 의사코드의 역할을 대신하는 중이다.
- 하지만 추상적인 내용들을 하나의 줄로 표현해야하는 경우, 의사코드가 효율적이라 할 수 있음 (파이썬 코드로 이를 표현할 시, 수십줄로 표현해야하는 경우가 있음).
- 알고리즘의 결과가 항상 동일한지, 실행에 따라 달라지는지 등에 따라 검증하는 방법이 다를 수 있다. 즉, 주어진 문제에 따라서 어떤 방식의 알고리즘을 설계할지 생각할 필요가있다.
'Study > 알고리즘' 카테고리의 다른 글
| 프로그래머가 알아야 할 알고리즘 40 Chapter 6 비지도 학습 알고리즘 (2) | 2022.11.23 |
|---|---|
| 프로그래머가 알아야 할 알고리즘 40 Chapter 5 그래프 알고리즘 (4) | 2022.11.16 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 4 알고리즘 설계 (6) | 2022.11.14 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 3 알고리즘에 사용되는 자료구조 (4) | 2022.10.31 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 2 알고리즘에 사용되는 자료구조 (1) | 2022.10.23 |