4장. 알고리즘 설계
요약
알고리즘을 설계할 때 중요한 포인트들과 여러 알고리즘 종류들을 알 수 있었다.
내용 정리
4.1 알고리즘 설계의 기본 개념 살펴보기
알고리즘 설계
- "특정 목표"를 가장 효율적으로 달성할 수 있는 "명료한 요구사항으로 구성된 유한한 집합"을 고안하는 것
- 문제 이해: 풀려는 문제를 명확히 이해해야 한다.
- 요구 사항: 무엇을 완료해야 하는지를 파악해야 한다.
- 알고리즘 설계: 어떻게 완료할 것인지 고민해야 한다.
문제 이해 단계
문제의 기능적 요구 사항과 비기능적 요구 사항을 모두 파악해야 한다.
- 기능적 요구사항: 문제의 입출력 인터페이스, 이와 관련된 함수를 의미함.
- 기능적 요구사항을 통해 기대하는 결과를 얻기 위해 구현해야 할 데이터 처리, 가공 및 연산과정을 이해
- 비기능적 요구사항: 알고리즘 성능과 보안에 관한 기대치를 설정
- 비기능적 요구사항을 통해 알고리즘 실행을 하면서 만족해야할 성능 등을 이해
기능적 요구사항과 비기능적 요구사항을 충족하는 알고리즘을 설계하기 위해 고려해야할 관점은 다음과 같다.
- 관점 1: 기대하는 결과를 출력하는가?
- 관점 2: 결과를 얻을 수 있는 최적의 방법인가?
- 관점 3: 큰 데이터 셋에서도 유효한 알고리즘인가?
관점 1 - 기대한 결과를 출력하는가?
결과를 검증하기 위해 두가지 측면을 고려해야 한다.
1. 정답 정의하기
- 정답(truth): 입력 데이터에 맞는 정확한 결과를 의미
- 알고리즘 검증에서 정답은 레퍼런스로 매우 중요한 역할을 수행한다.
2. 지표 선택하기
- 지표: 알고리즘이 출력한 답이 정답으로 부터 얼마나 벗어나는지를 정량화하는 척도
- 알고리즘 검증에서 지표를 통해 알고리즘 성능의 만족 기준을 정한다.
관점 2 - 결과를 얻을 수 있는 최적의 방법인가?
문제의 요구사항, 알고리즘을 실행하는데 필요한 자원을 명확히 이해해야 한다.
- 알고리즘이 요구사항을 정확히 충족하는지?
- 자원 내에서 주어진 문제를 알고리즘이 정상적으로 수행할 수 있는지?
문제의 성격과 복잡도를 이해하는 것이 매우 중요하다.
- 자원 요구사항을 측정하는데 도움이 된다.
알고리즘 관련 용어 정의
- 다항시간 알고리즘(polynomial time algorithm): 알고리즘 시간 복잡도가 O(n^k)이고, k가 상수인 알고리즘
- 증명서(certificate): 알고리즘이 개선되는 과정에서 생성되는 정답 후보들을 의미
- 딥러닝 같이 문제를 풀 때마다 생성되는 정답군들을 각각 증명서라 할 수 있다.
- 증명서의 값들이 점점 정답과 근접한 방향으로 수렴해 나가면 알고리즘이 개선되고 있다고 할 수 있다.
시간복잡도 분석은 두 가지 소요 시간을 측정한다.
- t_r: 알고리즘이 정답 후보(certificate)를 생성하는데 걸리는 시간
- t_s: 정답 후보(certificate)를 검증하는데 걸리는 시간
문제의 복잡도 파악하기
문제의 유형 파악
- 다항시간 알고리즘이 존재한다는 것이 보장된 문제
- 다항시간 알고리즘으로 풀 수 없다는 것을 증명할 수 있는 문제
- 다항시간 알고리즘을 찾아낼 수 없으며, 다항시간 알고리즘으로 문제를 해결할 수 없다는 것도 증명할 수 없는 문제
P / NP문제
- NP 문제 (비결정론적 다항시간, Non-deterministic Polynomial time)
- 정답 후보(증명서)가 최적이라는 것을 증명하는 다항시간 알고리즘이 존재
- P 문제 (다항시간, Polynomial time)
- NP문제의 하위 집합에 해당하는 문제
- 문제를 해풀 수 있는 다항시간 알고리즘이 최소 한개 이상 존재
컴퓨터 과학계에서 NP문제가 P와 동일한지는 아직 풀리지 않은 난제이다.
P와 NP 문제 외에도 두 가지 문제가 더 존재한다.
- NP-complete 문제 (NP 완전)
- NP 문제에서 가장 어려운 문제들로 구성된 하위 집합
- 해결책을 생성할 수 있는 다항 시간 알고리즘을 알 수 없다.
- 제안된 해결책이 최적인지 검증하는 다항시간 알고리즘이 존재한다.
- NP-hard 문제 (NP 난해)
- NP 집합에 속하지 않으면서 NP 집합에 있는 문제만큼 풀기 어려운 문제
P = NP인지, P != NP인지에 따라 아래처럼 도식화할 수 있다.

관점 3 - 큰 데이터 셋에서도 유효한 알고리즘인가?
좋은 알고리즘의 중요성은 빅데이터를 다룰 때 더 강조되는데, 잘 설계된 알고리즘은 확장성이 좋다는 특징이 있다.
알고리즘 확장성은 두 가지 측면에서 측정 가능하다.
- 공간 복잡도 분석
- 시간 복잡도 분석
4.2 알고리즘 설계 전략 이해하기
분할 및 정복 전략 이해
분할 및 정복 전략 (divide and conquer)
- 큰 문제를 독립된 여러 하위 문제로 쪼개서 푼 후, 결과를 상위 문제로 합치면서 상위 문제를 풀어내는 알고리즘
- ex> 아파치 스파크: 분할 정복 전략을 이용해 빅데이터 처리를 하는 오픈소스 프레임워크
- 마이크로소프트 애저, 아마존 AWS, 구글 클라우드 플랫폼 등 클라우드 컴퓨팅 인프라에서 주로 사용되는 전략
동적 계획법 (dynamic programming)
- 연산이 많은 작업 결과를 캐시에 저장해 재활용하는 전략
- 메모이제이션(memoization): 동적 계획법에서 활용하는 캐싱 메커니즘을 칭하는 말
- 풀려는 문제가 여러 하위 문제로 구성되고, 하위 문제 끼리 푸는 연산 작업이 반복되고, 결과를 서로 공유해야 할 때 유용함
- 입력 데이터를 반복 처리하는 재귀 구조를 가진 문제에서 강력한 성능을 발휘함
탐욕 알고리즘 (greedy algorithm)
- 지금 주어진 상황에서 최적의 해를 찾는 방법
- 정확한 정답을 찾진 못할 수 있으나 알고리즘 연산 속도를 최대한 줄이는 방법
- 많은 경우의 수를 실행할 수 없는 경우에 유용하게 사용됨
- 알고리즘 오버헤드를 최소화 하는 방식이다.
탐욕 알고리즘의 장점
- 최적해를 빠르고 간단하게 찾는 방법이다.
- 알고리즘은 분기마다 최선의 안을 선택한다.
- 분할 및 정복 전략이나 동적 계획법에 비해 계산 속도가 훨씬 빠르다.
- 어느정도 작동 가능한 해결책이 필요한 경우 유용히 사용할 수 있다.
탐욕 알고리즘의 단점
- 분기마다 선택한 최선의 안이 전체적(전역적)으로 최적인지는 확인하지 않는다.
- 특별한 경우가 아닌 경우, 일반적으로 전역적 최적해를 얻을 수 없다.
탐욕 알고리즘 과정
- 데이터셋 D에서 요소 k를 선택한다.
- 정답 후보 S가 k를 포함하는지 확인한다. 포함 여부는 현재 상황에서 k를 포함하는게 최적인지에 대한 판단으로 이루어진다. 만약 k가 S에 포함되면 해결책은 합집합 (S, k)가 된다.
- S가 다 채워지거나 D의 모든 요소를 확인할 때까지 이 과정을 반복한다.
용어 정리
알고리즘 오버헤드(algorithmic overhead)
- 어떤 문제의 최적 해결책을 찾는데 걸리는 시간
최적해와의 차이(delta from optimal)
- 최적해(optimal solution)가 알려진 경우, 현재 해결책과 최적해와의 차이를 통해 해결책을 나은 방향으로 개선할 수 있다.
4.3 활용 사례 - 외판원 문제 해결하기
외판원 문제(TSP, Traveling Salesman Problem)
- 판매원(외판원)은 주어진 도시들을 모두 방문해야하며, 최단 거리로 방문하기를 원한다.
- 방문해야 하는 도시와 도시간 거리는 주어진다. 그리고 모든 도시는 한 번만 방문해야 한다.
- 방문해야 하는 도시 수가 늘어날 수록 경우의 수는 기하급수적으로 증가하기 때문에 최적해를 구하기 어렵다.
- NP-난해 문제이다.
외판원 문제 도시, 도시간 거리 생성 및 거리 계산 함수 구현
import random
from itertools import permutations
def distance_points(first, second): return abs(first - second)
def distance_tour(aTour):
return sum(distance_points(aTour[i - 1], aTour[i]) for i in range(len(aTour)))
def generate_cities(number_of_cities):
seed = 111
width = 500
height = 300
random.seed((number_of_cities, seed))
return frozenset(aCity(random.randint(1, width), random.randint(1, height))
for c in range(number_of_cities))
alltours = permutations
aCity = complex
무차별 대입 전략 사용
무차별 대입 전략(brute-force strategy)
- 가능한 투어 일정들을 무작위로 생성하고, 이동거리가 가장 짧은 투어 일정을 정한다.
- n개의 도시를 순회하는 모든 경우의 수는 (n-1)!개로 방문해야 할 도시 수가 늘면 연산 수가 매우 크게 증가한다.
- 따라서 도시 수가 일정 수 이상으로 커지면 실제 실행하기는 어려운 알고리즘이다.
무차별 대입 전략 코드 구현
import time
from collections import Counter
def shortest_tour(tours): return min(tours, key = distance_tour)
def brute_force(cities):
"""모든 가능한 투어를 생성한 다음 이동 거리가 가장 짧은 투어를 선택"""
return shortest_tour(alltours(cities))
## 시각화 관련 코드
%matplotlib inline
import matplotlib.pyplot as plt
def X(city): "X axis"; return city.real
def Y(city): "Y axis"; return city.imag
def visualize_segment(segment, style = 'bo-'):
plt.plot([X(c) for c in segment], [Y(c) for c in segment], style, clip_on = False)
plt.axis('scaled')
plt.axis('off')
def visualize_tour(tour, style = 'bo-'):
if len(tour) > 1000: plt.figure(figsize = (15, 10))
start = tour[0:1]
visualize_segment(tour + start, style)
visualize_segment(start, 'rD')
## 무차별 대입전략 tsp 적용
def name(algorithm): return algorithm.__name__.replace('_tsp', '')
def tsp(algorithm, cities):
t0 = time.perf_counter()
tour = algorithm(cities)
t1 = time.perf_counter()
assert Counter(tour) == Counter(cities) # 모든 도시는 한번만 등장해야 함.
visualize_tour(tour)
print(f"{name(algorithm)}:{len(tour)} cities = tour length {distance_tour(tour)} (in {t1 - t0} sec)")
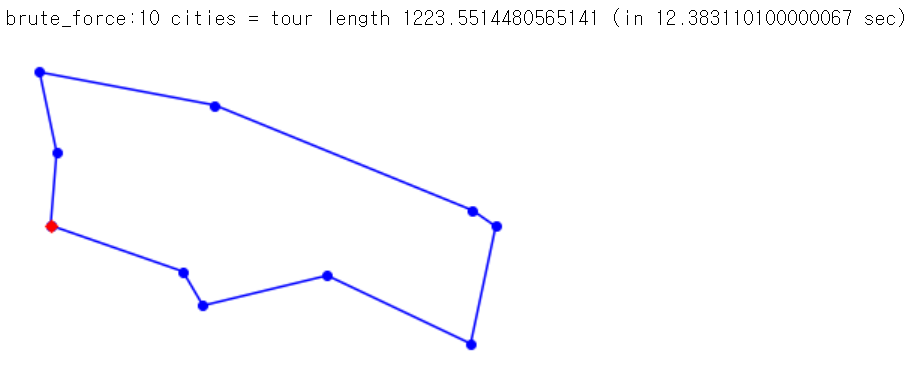
tsp(brute_force, generate_cities(10))
코드의 실행 결과는 아래와 같다.
탐욕 알고리즘 사용
탐욕 알고리즘은 현 위치에서 가장 가까운 도시로 이동한다.
- 전체 관점에서 최적인 도시를 선택하는게 아니라, 매 순간 상황마다 최적인 도시를 다음 방문지로 선택한다.
- 장점: 무차별 대입 전략에 비해 알고리즘 실행 속도가 매우 빠르다.
- 단점: 전체 투어 관점에서는 최적의 선택이 아닐 확률이 크다.
탐욕 알고리즘 과정
- 출발지를 무작위로 선택
- 현 위치에서 방문한 적 없으면서 가장 가까운 도시로 이동
- 단계 2를 반복
탐욕 알고리즘 코드 구현
def first(collection): return next(iter(collection))
def nearest_neighbor(A, cities):
return min(cities, key = lambda C: distance_points(C, A))
def greedy_algorithm(cities, start = None):
C = start or first(cities)
tour = [C]
unvisited = set(cities - {C})
while unvisited:
C = nearest_neighbor(C, unvisited)
tour.append(C)
unvisited.remove(C)
return tour
tsp(greedy_algorithm, generate_cities(2000))
위 코드의 결과는 다음과 같다.

4.4 페이지랭크 알고리즘 이해하기
페이지랭크(PageRank) 알고리즘
- 인터넷 검색 서비스 구글이 사용자 검색어에 따른 결과 순서를 매기는 용도로 고안한 알고리즘
- 알고리즘은 사용자가 입력한 검색어 맥락을 바탕으로 검색 결과의 중요도를 수치화함
- 래리 페이지와 세르게이 브린이 개발하였음
페이지랭크 알고리즘 이해
검색된 페이지들의 중요도를 계산하는 최적의 방법을 찾아야 한다.
검색된 단어와 페이지간 중요도를 0 ~ 1 사이의 숫자로 표현하기 위해 다음 두가지 정보를 활용한다.
- 사용자가 입력한 검색어와 관련한 정보
- 사용자가 입력한 검색어 맥락과 검색된 페이지 내용이 얼마나 서로 연관돼 있는지 추정
- 페이지 자체와 관련된 정보
- 페이지가 가진 링크, 조회 수, 이웃의 수 등을 이용해 페이지가 가진 중요도를 정량화 함
페이지 랭크 알고리즘 구현
다섯 개 페이지가 등록된 간단한 네트워크를 생성
- myPages: 페이지 리스트를 담은 변수
- myWeb: 네트워크
# 네트워크 생성
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
myWeb = nx.DiGraph()
myPages = range(1, 5)
connections = [(1, 3), (2, 1), (2, 3), (3, 1), (3, 2), (3, 4), (4, 5), (5, 1), (5, 4)]
myWeb.add_nodes_from(myPages)
myWeb.add_edges_from(connections)
pos = nx.shell_layout(myWeb)
nx.draw(myWeb, pos, arrows = True, with_labels = True)
plt.show()
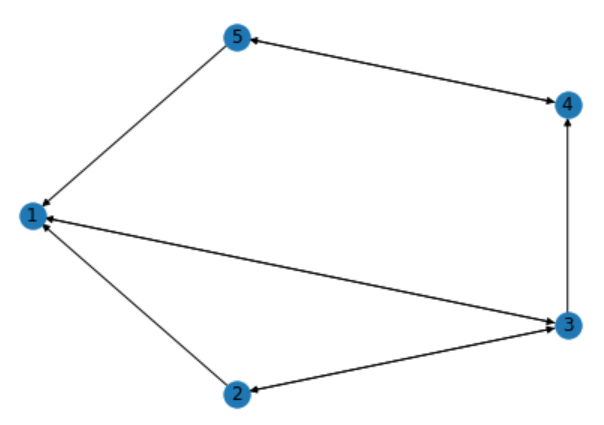
페이지랭크 알고리즘은 웹 페이지 패턴을 전이 행렬(transpose matrix)로 표현
- 전이 행렬은 n X n 크기로 나타나고, n은 노드의 개수이다.
- 전이 행렬의 수치는 한 노드에서 다른 노드로 이동할 확률을 의미한다.
def createPageRank(aGraph):
nodes_set = len(aGraph)
M = nx.to_numpy_matrix(aGraph)
outwards = np.squeeze(np.asarray(np.sum(M, axis = 1)))
prob_outwards = np.array([1.0/count if count > 0 else 0.0 for count in outwards])
G = np.asarray(np.multiply(M.T, prob_outwards))
p = np.ones(nodes_set) / float(nodes_set)
if np.min(np.sum(G, axis = 0)) < 1.0:
print('경고: 전이 확률 합의 최솟 값이 1보다 작습니다.')
return G, p
G, p = createPageRank(myWeb)
print(G)
>> [[0. 0.5 0.33333333 0. 0.5 ]
[0. 0. 0.33333333 0. 0. ]
[1. 0.5 0. 0. 0. ]
[0. 0. 0.33333333 0. 0.5 ]
[0. 0. 0. 1. 0. ]]
- 자기 자신으로 돌아오는 노드가 없기 때문에 행렬의 대각성분은 모두 0이다.
- 전이 행렬은 0 값이 많은 희소 행렬(sparse matrix)이다. 노드 수가 많아질수록 전이 확률이 0인 값들이 증가한다.
4.5 선형 계획법 이해하기
선형 계획법(linear programming)
- 어떤 제약조건들이 주어졌을 때 목적 함수를 최소화하거나 최대화 시키는 문제에 적합한 방법론
선형 계획법의 조건
- 목적 함수 정의하기: 목적함수는 다른 변수들의 선형 함수로 표현되며, 목적 함수를 최소화/최대화 하는 것이 목표이다.
- 제약 조건 설정하기: 문제가 만족해야 하는 제약 조건들을 설정한다.
- 문제는 방정식의 집합으로 표현된다.
- 방정식에 사용되는 변수들은 일차 방정식 관계로 나타낸다.
4.6 활용 사례 - 선형 계획법을 활용해 용량 계획하기
선형 계획법을 이용해서 아래 목적 함수 최대화하기
- 목적 함수: Max (5000A + 2500B)
- 제약조건
- A >= 0
- B >= 0
- 3A + 2B <= 20
- 4A + 3B <= 30
- 4A + 3B <= 44
선형 계획법 코드 구현
import pulp
model = pulp.LpProblem("Profit maximising problem", pulp.LpMaximize)
A = pulp.LpVariable('A', lowBound = 0, cat = 'Integer')
B = pulp.LpVariable('B', lowBound = 0, cat = 'Integer')
# 목적 함수 정의
model += 5000 * A + 2500 * B, "Profit"
# 제약 조건 설정
model += 3 * A + 2 * B <= 20
model += 4 * A + 3 * B <= 30
model += 4 * A + 3 * B <= 44
# 풀이
model.solve()
pulp.LpStatus[model.status]
# 결정 변수들의 값 출력
print(A.varValue)
>> 6.0
print(B.varValue)
>> 1.0
# 목적 함수의 값 출력
print(pulp.value(model.objective))
>> 32500.0
선형계획법은 자원 활용을 최적화해서 생산성을 높일 수 있는 도구로 다양한 제조업 분야에서 사용되고 있다.
'Study > 알고리즘' 카테고리의 다른 글
| 프로그래머가 알아야 할 알고리즘 40 Chapter 6 비지도 학습 알고리즘 (2) | 2022.11.23 |
|---|---|
| 프로그래머가 알아야 할 알고리즘 40 Chapter 5 그래프 알고리즘 (4) | 2022.11.16 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 3 알고리즘에 사용되는 자료구조 (4) | 2022.10.31 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 2 알고리즘에 사용되는 자료구조 (1) | 2022.10.23 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 1 알고리즘 기초 (0) | 2022.10.21 |