2장. 알고리즘에 사용되는 자료구조
요약
파이썬에 내장된 자료구조들의 특징과 이를 이용해 구현할 수 있는 추상화 자료형들에 대해 학습할 수 있었다.
내용 정리
2.1 파이썬 자료 구조 파악하기
알고리즘을 실행할 때는 데이터를 보관할 인메모리 자료구조가 필요함
=> 적절한 자료구조를 선택하는 것은 효율적인 알고리즘 구현의 필수요소이다.
- 자료구조(Data structure): 컬렉션을 저장하는 방법론들을 통칭함
- 컬렉션(collection): 특정 목적을 위해 함께 저장되고 처리되는 데이터 요소들의 묶음
- 파이썬의 자료구조 종류
- 리스트(list): 데이터 요소간 순서가 있고, 수정이 가능한 자료구조
- 튜플(tuple): 데이터 요소간 순서는 있으나 수정이 불가한 자료구조
- 세트(set): 데이터 요소간 순서가 없고 중복이 없는 자료구조
- 딕셔너리(dictionary): 데이터 요소간 순서가 없는 키-값 쌍의 묶음
- 데이터프레임(dataframe): 이차원 데이터를 저장하는 이차원 구조
리스트(list)
- 리스트에 저장되는 자료 유형들은 모두 같지 않아도 된다.
- 데이터 요소들을 [] 안에 넣고 쉼표로 구분하게 된다.
- 가변 자료 구조로 요소의 추가/삭제가 가능하다는 장점이 있지만 그만큼 불변 자료 구조에 비해 비용이 발생한다.
list_a = ['John', 33, "Toronto", True] # 리스트내 요소들의 자료형이 달라도 상관없다.
print(list_a)
>> ['John', 33, "Toronto", True]
- 리스트 인덱싱(list indexing): 위치 값(인덱스)을 이용해서 리스트 특정 위치에 존재하는 요소 값에 접근하는 방법
bin_colors = ["Red", "Green", "Blue", "Yellow"]
bin_colors[1] # 리스트의 위치는 0부터 시작한다.
>> "Green"
- 리스트 슬라이싱(list slicing): 인덱스 범위를 설정하여 해당 인덱스에 속하는 값들을 가져오는 것
bin_colors = ["Red", "Green", "Blue", "Yellow"]
bin_colors[0:3] # 슬라이싱 시, 마지막 인덱스 값을 제외한 범위까지의 요소들을 가져온다.
>> ["Red", "Green", "Blue"]
bin_colors[2:] # 마지막 인덱스를 생략하면 첫번째 인덱스부터 마지막 위치의 요소까지 가져온다.
>> ["Blue", "Yellow"]
bin_colors[:2] # 첫번째 인덱스를 생략하면 0번째 위치의 요소부터 마지막 인덱스 위치 전까지의 요소들을 가져온다.
>> ["Red", "Green"]
- 네거티브 인덱싱(negative indexing): 리스트의 끝에서부터 거꾸로 위치를 세는 음수 인덱스를 의미함
- 인덱스 기준을 리스트 끝위치부터 생각할 때 유용하게 사용될 수 있음
bin_colors = ["Red", "Green", "Blue", "Yellow"]
bin_colors[:-1] # -1은 리스트 끝 위치의 인덱스 위치를 의미함. 즉, 리스트 끝 위치 전까지 요소를 가져옴
>> ["Red", "Green", "Blue"]
bin_colors[:-2]
>> ["Red", "Green"]
bin_colors[-2:-1]
>> ["Blue"]
- 내포(nesting): 리스트 내에 리스트나 다른 자료구조를 넣는 것을 의미
- 반복적이거나 재귀적인 알고리즘을 사용할 때 내포를 유용하게 사용할 수 있음
a = [1, 2, [100, 200, 300], 6]
max(a[2])
>> 300
a[2][1]
>> 200
- 반복(iteration): 파이썬의 for 루프문을 통해서 리스트 안에 든 요소들을 반복적으로 처리할 수 있다.
bin_colors = ["Red", "Green", "Blue", "Yellow"]
for color in bin_colors:
print(color + " Square")
>> Red Square
Green Square
Blue Square
Yellow Square
- 리스트의 시간 복잡도
| 연산작업 | 시간 복잡도 |
| 요소 삽입 | O(1) |
| 요소 제거 | O(n) |
| 리스트 슬라이싱 | O(n) |
| 요소 접근 | O(1) |
| 복사 | O(n) |
- 요소 제거는 특정 위치의 값을 제거하고 다시 리스트를 재구성하기 때문에 O(n)만큼 소요
- 슬라이싱도 전체 리스트를 다가져오면 O(n)이다.
- 특정 요소에 접근 시, 해당 index 위치로 접근이 바로 가능하기 때문에 O(1)이다.
람다 함수 (Lambda function)
- 함수를 즉시 생성할 수 있으며 알고리즘에서 매우 중요한 역할
- 익명 함수(anonymous function)으로도 불림
- 데이터 필터링 (Data filtering)
- 조건함수를 람다 함수로 설정해 데이터 필터링을 할 수 있다.
- 파이썬의 필터(filter) 함수는 일반적으로 람다 함수와 함께 사용된다.
list(filter(lambda x: x > 100, [-5, 200, 300, -10, 10, 1000]))
>> [200, 300, 1000]
func = lambda x: x > 100
func([-5, 200, 300, -10, 10, 1000])
>> [False, True, True, False, False, True] # Boolean 값으로 조건에 만족하는지 출력
- 데이터 변환
- map 함수를 이용해 데이터들을 변환함
- 람다 함수로 변환 방식을 설정하고, map 함수는 각 요소들에 변환 방식을 각각 적용함
list(map(lambda x: x ** 2, [11, 22, 33, 44, 55]))
>> [121, 484, 1089, 1936, 3025]
- 데이터 집계
- 리듀스(reduce) 함수를 사용하며, 리스트를 순회하며 값 쌍을 재귀적으로 처리하게 된다.
from functools import reduce
x = reduce(lambda x, y: x + y, [100, 122, 33, 4, 5, 6])
print(x)
>> 240
Range 함수
- 반복적으로 수가 커지거나 작아지는 수의 리스트를 생성할 수 있는 함수
# 숫자를 하나만 선언하면 0부터 1씩 증가하며, 해당숫자의 크기만큼의 요소가 담기게 된다.
x = range(6) # 해당 숫자 전까지의 값이 담긴다고 생각할 수 있다.
list(x)
>> [0, 1, 2, 3, 4, 5] # 0부터 5까지 6개 요소가 담긴 리스트
# 시작할 값부터 어디까지, 그리고 건너뛸 크기값을 설정할 수도 있다.
oddNums = range(3, 29, 2)
list(oddNums)
>> [3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27] # 마지막 숫자였던 29는 담지 않는다.
튜플(Tuple)
- 수정할 수 없는 자료구조로 선언 후에는 읽기만 가능하다.
- 튜플은 ()로 감싸서 생성한다.
- 여러 자료 유형들을 요소들로 가질 수 있으며, 내포도 가능함
bin_colors = ("Red", "Green", "Blue", "Yellow")
bin_colors[1]
>> "Green"
bin_colors[2:]
>> ("Blue", "Yellow")
bin_colors[:-1]
>> ("Red", "Green", "Blue")
# 내포(nesting)의 예시
a = (1, 2, (100, 200, 3000), 6) # 이중 튜플 자료 구조의 예시
max(a[2])
>> 300
a[2][1]
>> 200
- 성능 향상을 위해서는 리스트와 같은 가변 자료 구조보다 튜플과 같은 불변 자료 구조가 효율적이다.
- 특히 대규모 데이터인 경우 불변 자료 구조를 사용하면 처리 속도를 크게 향상할 수 있다.
- 따라서 데이터가 추가/삭제될 필요가 없다면 읽기 전용인 튜플과 같은 불변 자료 구조를 이용하여 처리 속도를 높이는 것이 바람직하다.
딕셔너리(Dictionary)
- 데이터를 키-쌍 값으로 저장하기 때문에 데이터를 가장 잘 식별할 수 있는 키값 지정이 필요하다.
- 키는 숫자, 문자열 등을 지정할 수 있다.
- 값으로는 수, 문자열, 자료구조 등 다양하게 설정할 수 있다.
- 키-값 쌍을 {}로 감싸서 선언한다.
bin_colors = {
"manual_color": "Yellow",
"approved_color": "Green",
"refused_color": "Red"
}
print(bin_colors)
>> {"manual_color": "Yellow", "approved_color": "Green", "refused_color": "Red"}
# 키를 사용해 값에 접근하는 법
bin_colors.get('approved_color') # (1) get 함수를 사용
>> "Green"
bin_colors['approved_color'] # (2) 해당 키를 인덱스로 사용
>> "Green"
# 키를 사용해 값을 갱신하는 법
bin_colors['approved_color'] = 'black'
bin_colors['approved_color']
>> 'black'
- 딕셔너리의 시간 복잡도
| 연산 작업 | 시간 복잡도 |
| 키 또는 값에 접근 | O(1) |
| 키 또는 값을 설정 | O(1) |
| 딕셔너리 복사 | O(n) |
세트(Set)
- 세트도 {}로 묶여있으나 요소들만 나열돼 있다.
- 중복된 요소들이 없으며, unique한 요소들의 컬렉션으로 구성된다.
green = {'grass', 'leaves'}
print(green)
>> {'grass', 'leaves'}
# 세트는 요소의 중복을 허용하지 않는다.
green = {'grass', 'leaves', 'grass', 'leaves'}
print(green)
>> {'grass', 'leaves'}
- 세트는 합집합(union)과 교집합(intersection)을 지원한다.
- 합집합은 | 로, 교집합은 &로 나타낸다.
yellow = {'a', 'b', 'c', 'd'}
red = {'b', 'd', 'e', 'f'}
# 합집합
yellow | red
>> {'a', 'b', 'c', 'd', 'e', 'f'}
# 교집합
yellow & red
>> {'b', 'd'}
- 세트의 시간 복잡도
| 연산 작업 | 시간 복잡도 |
| 요소 추가 | O(1) |
| 요소 제거 | O(1) |
| 복사 | O(1) |
- 세트의 요소는 해시로 표현되기 때문에 모두 O(1)로 처리가 가능하다.
데이터프레임(dataframe)
- 파이썬 pandas 라이브러리에서 제공하는 자료 구조
- 테이블형 데이터를 저장하는데 널리 사용됨
import pandas as pd
df = pd.DataFrame([
[1, 'Fares', 32, True],
[2, 'Elena', 23, False],
[3, 'Steven', 40, True]])
df.columns = ['id', name', 'age', 'decision']
df
>>
id name age decision
0 1 Fares 32 True
1 2 Elena 23 False
2 3 Steven 40 True
- 축(axis): 개별 열(column)이나 행(row)를 의미
- 축들(axes): 축 2개이상을 지칭
- 라벨(label): 열과 행에 이름을 짓는 것
- 데이터프레임도 인덱싱과 필터가 가능
행렬(matrix)
- 고정된 수의 열과 행을 가지는 이차원 자료 구조
- 행과 열 정보로 인덱싱하여 요소에 접근 가능
- 멀티미디어 데이터를 처리할 때 많이 사용됨
myMatrix = np.array([
[11, 12, 13],
[21, 22, 23],
[31, 32, 33]])
print(myMatrix)
>> [[11, 12, 13],
[21, 22, 23],
[31, 32, 33]]
print(type(myMatrix))
>> <class 'numpy.ndarray'>- transpose 함수를 통해 행렬을 전치할 수 있다.
2.2 추상화 자료 유형 파악하기
- 추상화(abstraction): 공통적인 핵심 함수를 사용해서 복잡한 시스템을 정의하는 개념
- 추상화 자료 유형(Abstract Data Type, ADT): 자료 구조에 추상화 개념을 적용한 것
- 장점: 디테일한 세부 내용을 숨겨서 사용자가 인터페이스를 사용함 => 깔끔하고 단순한 코드로 알고리즘을 구현할 수 있음
- 여러 프로그래밍 언어들로 동일한 추상화 자료 유형을 구현할 수 있음
벡터(Vector)
- 데이터를 저장하는 일차원 자료 구조
- 표현 방법
- 파이썬 리스트로 표현
- numpy 배열 사용하기
스택(Stack)
- 일차원 리스트를 저장하는 선형 자료 구조
- 스택은 저장할 요소들을 후입선출(Last-In-First-Out, LIFO) 또는 선입후출(First-In-Last-Out, FILO)하는 방식이라 할 수 있다.
- 연산 종류
- isEmpty: 비어있는지 여부를 출력
- push: 새 요소를 스택에 추가
- pop: 최근에 추가한 요소를 스택에서 제거하고 반환
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
# Stack 인스턴스 생성
stack = Stack()
stack.push('Red')
stack.push('Blue')
stack.pop()
>> 'Blue'- 각 연산의 시간복잡도는 모두 O(1)이다.
- 활용 사례
- 웹 브라우저에서 사용자의 검색 기록을 조회할 때 보이는 데이터
- 워드프로세서 소프트웨어에서 제공하는 실행 취소(Undo) 기능
큐(Queue)
- 일차원 자료 구조로 선입후출(First-In-First-Out, FIFO) 형식으로 데이터가 추가/제거됨
- 추가/제거하는 연산을 enque/deque라 부름
class Queue(object):
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0, item)
def deque(self):
return self.items.pop()
def size(self):
return len(self.items)
queue = Queue()
queue.enqueue('a')
queue.enqueue('b')
queue.dequeue()
>> 'a'
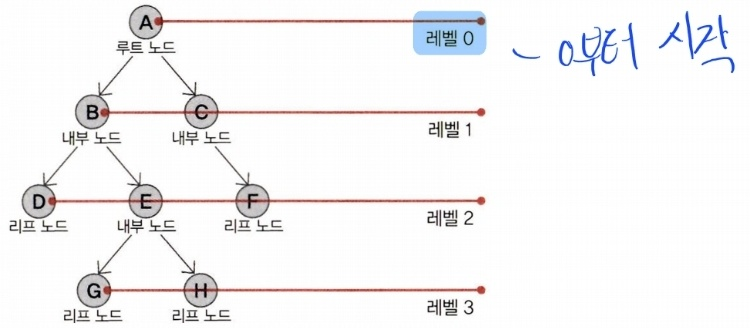
트리(Tree)
- 계층적 데이터를 저장할 수 있는 자료 구조로 각 트리는 유한한 수의 노드(node)로 구성됨
- 루트(root): 트리의 시작이 되는 요소
- 브랜치(branch): 노드와 노드 사이의 연결선
- 트리 관련 용어
| 용어 | 설명 |
| 루트 노드 | 가장 최상단의 노드로 루트 노드의 부모는 없다. |
| 노드 레벨 | 루트 노드부터 특정 노드까지의 거리. 깊이라고도 칭한다. |
| 형제 노드 | 노드의 레벨이 동일하고 부모 노드가 같은 노드들 |
| 부모 노드와 자식 노드 | 특정 노드의 부모는 부모노드. 본인은 부모노드의 자식 노드 |
| 노드의 차수(degree) | 해당 노드가 가진 자식 노드의 수 |
| 트리의 차수 | 트리를 구성하는 모든 노드가 가진 차수들 중 최댓값 |
| 하위(sub) 트리 | 선택한 노드를 루트노드로 하여 트리를 다시 구성 |
| 리프(leaf) 노드 | 말단 노드들로 자식 노드가 없는 경우 |
| 내부(internal) 노드 | 루트나 리프노드가 아닌 나머지 노드들 |
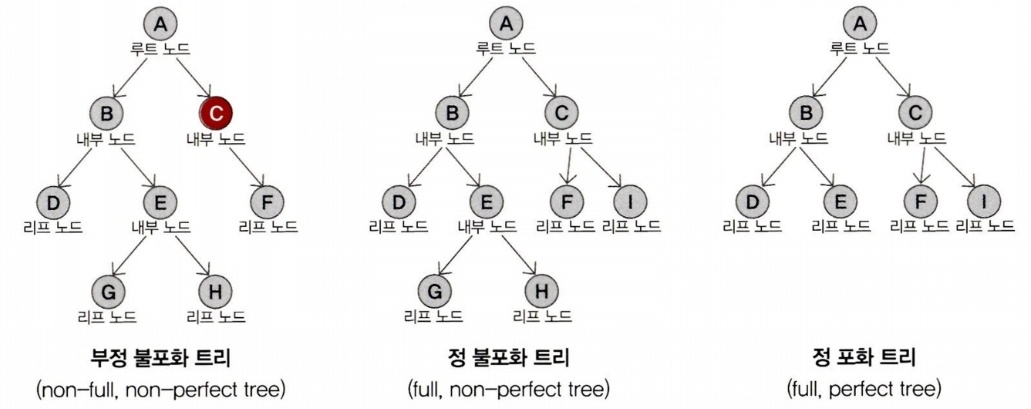
- 트리의 유형
- 이진 트리(binary tree): 트리의 차수가 2인 트리
- 정 트리(full tree): 정 트리의 노드들은 모두 같은 차수를 가짐
- 포화 트리(perfect tree): 정 트리의 특수 형태로, 모든 리프 노드가 동일한 레벨을 가지게 됨
- 순서 트리(ordered tree): 특정 기준에 맞추어 자식 노드들이 정렬된 트리
- 활용 사례
- 지도 학습 알고리즘
- 네트워크 분석 알고리즘
- 부할 및 정복 전략(divide and conquer strategy)에 기반한 다양한 정렬 및 검색 알고리즘 등
2.3 요약
- 알고리즘에 사용할 적절한 자료 구조를 선택할 수 있어야 한다.
- 어떤 자료 구조를 선택하는지에 따라 알고리즘의 성능에 차이가 날 수 있다.
- 자료 구조가 알고리즘 성능에 미치는 영향을 이해할 수 있어야 한다.
학습 후기
- 알고리즘의 로직은 이전에 의사코드(pseudocode)로 작성되었지만 최근에는 파이썬 코드가 의사코드의 역할을 대신하는 중이다.
- 하지만 추상적인 내용들을 하나의 줄로 표현해야하는 경우, 의사코드가 효율적이라 할 수 있음 (파이썬 코드로 이를 표현할 시, 수십줄로 표현해야하는 경우가 있음).
- 알고리즘의 결과가 항상 동일한지, 실행에 따라 달라지는지 등에 따라 검증하는 방법이 다를 수 있다. 즉, 주어진 문제에 따라서 어떤 방식의 알고리즘을 설계할지 생각할 필요가있다.
'Study > 알고리즘' 카테고리의 다른 글
| 프로그래머가 알아야 할 알고리즘 40 Chapter 6 비지도 학습 알고리즘 (2) | 2022.11.23 |
|---|---|
| 프로그래머가 알아야 할 알고리즘 40 Chapter 5 그래프 알고리즘 (4) | 2022.11.16 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 4 알고리즘 설계 (6) | 2022.11.14 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 3 알고리즘에 사용되는 자료구조 (4) | 2022.10.31 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 1 알고리즘 기초 (0) | 2022.10.21 |