Chapter 06. 비지도 학습 알고리즘
요약
비지도 학습의 여러 알고리즘들을 학습하고 어떻게 활용되는지 알 수 있었다.
내용 정리
6-1. 비지도 학습 이해하기
비지도 학습 (Unsupervised learning)
- 데이터에 내재된 패턴을 발견하고 이를 구조화하는 프로세스
- 데이터가 무작위로 생성된 것이 아닌 이상, 다차원의 공간에서 데이터 요소 간에는 어떤 패턴이 존재한다.
- 비지도 학습은 숨겨진 패턴을 찾아내 데이터셋에 구조를 부여하는 과정이다.
- 지도 학습과 비지도 학습을 결합해 새로운 알고리즘을 개발하려는 연구자들이 늘고 있다 (semi-supervised learning).
비지도 학습의 장점
- 정답이 주어져 있지 않기 때문에 분석이 훨씬 유연해 가정(assumption)에 덜 의존적임
- 어떤 차원의 데이터든 결과가 잠재적으로 수렴할 수 있음
- 숨겨진 패턴을 찾아낼 수 있는 잠재력이 있음
비지도 학습의 단점
- 지도 학습에 비해 요구사항과 범위를 조정하기 힘듦
비지도 학습의 활용 사례
- 음성 분류
- 각 개인의 음성은 분류할 수 있는 패턴, 특성이 있는 점을 이용해서 분류
- 서로 다른 사람의 음성을 구분할 수 있게 분류 모델을 훈련함
- 비지도 학습은 주어진 비정형 데이터에 구조를 부여하고, 우리가 가진 문제 공간(특성)에 새로운 차원을 추가할 수 있게함
- 문서 분류
- 문서의 내용에 따라 주제를 분류
데이터 마이닝 사이클에서 비지도 학습
데이터 마이닝 프로세스의 방법론
- CRISP-DM 라이프 사이클 (Cross-Industry Standard Process for Data Mining)
- 크라이슬러, SPSS 등 여러 회사에 속한 데이터 마이너 전문가들이 제안한 방법론
- SEMMA 데이터 마이닝 프로세스 (Sample, Explore, Modify, Model, Access)
- SAS 회사가 제안한 방법론
CRISP-DM 라이프 사이클
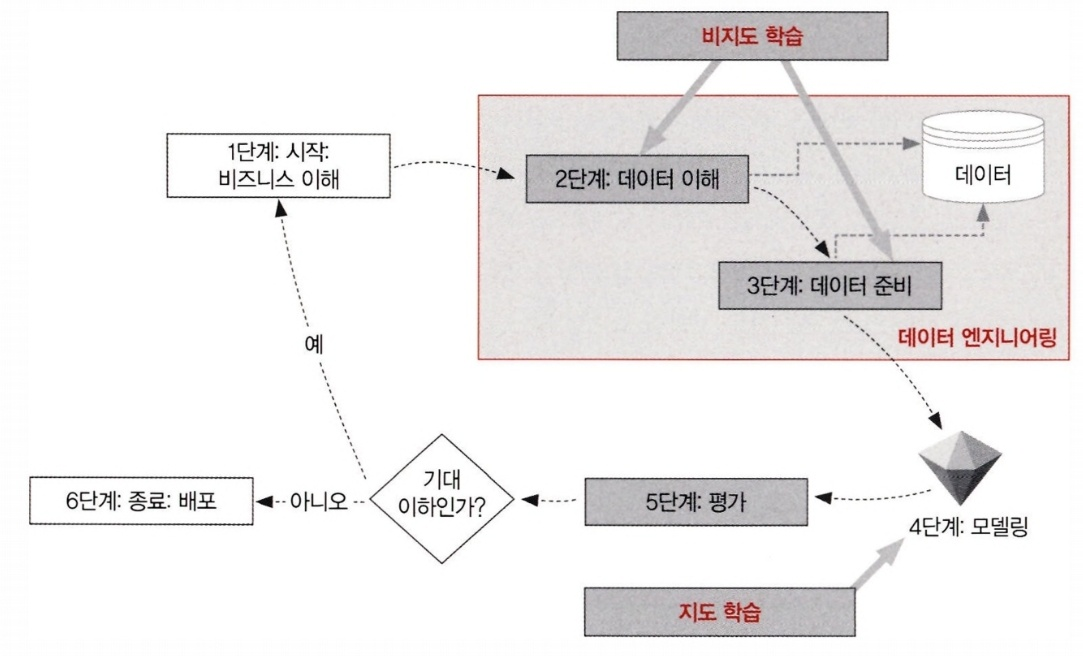
- 비지니스 이해
- 비지니스 관점에서 문제와 요구사항을 세밀하게 이해하는 단계
- 문제의 범위를 정의하고 머신러닝이 풀 수 있게 문제를 재정의하는게 중요함
- 어떻게 풀지가 아니라 무엇을 풀지를 정의하는게 중요한 단계
- 최소 정확도 등 여러 지표의 머신러닝 모델의 기대 성능을 정의함
- 데이터 이해
- 데이터 마이닝에 사용할 데이터를 이해하는 단계
- 풀려는 문제에 적합한 데이터가 있는지, 데이터의 품질과 구조는 어떤지, 유의미한 패턴이 있을지 등을 파악
- 문제 해결을 위한 라벨 또는 타깃 변수가 존재하는지 파악. 있으면 지도학습, 없으면 비지도학습임
- 데이터 준비
- 머신러닝 훈련에 필요한 데이터를 준비하는 단계
- 모델을 학습할 훈련 데이터(training data)와 모델을 평가할 평가 데이터(testing data)로 분리한다. 보통 학습 데이터의 데이터 비중이 더 크다.
- 비지도 학습은 데이터 준비 단계에 사용될 수 있다. 비지도학습을 통해 패턴을 추출해 데이터의 특성을 생성할 수 있다.
- 모델링
- 앞서 발견한 패턴을 활용해서 지도 학습을 수행하는 단계
- 타겟 변수와 특성 사이의 관계를 수학적 공식으로 구성하며, 알고리즘에 따라 수학적 공식은 달라진다.
- 알고리즘은 훈련 데이터로 학습된다.
- 평가
- 모델의 성능을 평가하는 단계
- 테스트 데이터로 성능이 평가된다.
- 알고리즘 성능이 기대 성능에 만족하지 못하면 1단계로 돌아간다.
- 배포
- 모델을 프로덕션 환경에 배포하는 단계다.
- 1단계에서 정의한 문제에 대한 솔루션을 제공하는 단계다.
데이터 엔지니어링
- 데이터 이해(2단계)와 데이터 준비(3단계) 과정을 위해 데이터 엔지니어가 고용될 수 있다.
- 데이터 엔지니어는 데이터 전처리, 가공, 클렌징 등 과정을 수행한다.
- 머신러닝에서 가장 시간이 많이 드는 과정이라 할 수 있다.
- 비지도 학습은 데이터 이해 및 엔지니어링에 있어 중요한 역할을 한다.
6-2. 클러스터링 알고리즘 이해하기
클러스터링(clustering)
- 비슷한 패턴의 데이터끼리 그룹을 묶는 비지도 학습 알고리즘
- 문제와 관련된 데이터 특정 부분들을 이해하는데 사용
- 유사도(similarity)를 활용해 데이터 포인트간 그루핑(grouping)을 진행함
- 유사도를 계산하는 최적의 방식은 문제마다 다르며, 문제 성격에 적합한 유사도 계산 방식을 선택해야 함
- 생성된 그룹의 안정성은 데이터 포인트 간 유사도나 거리를 적합하게 정량화가 될수록 커진다.
주로 사용되는 유사도 계산 방식
- 유클리드 거리
- 맨해튼 거리
- 코사인 거리
유클리드 거리(Euclidean distance)
- 다차원 공간의 두 포인트 사이의 가장 짧은 거리
- n차원인 두 점 A와 B가 주어졌을 때 A와 B의 유클리드 거리는 다음과 같다.

맨해튼 거리(Manhatten distance)
- 두 점 사이의 가장 긴 경로를 표현하는 거리
- 맨해튼 거리는 항상 유클리드 거리보다 크거나 같다.
코사인 거리(cosine distance)
- 원점에 연결된 두 포인트가 만들어내는 각도의 코사인 값을 계산해 거리를 계산함
- 유클리드 거리나 맨해튼 거리보다 고차원 공간에서 두 포인트 사이 거리를 정확히 잴 수 있다.
- 코사인 거리는 보통 고차원인 텍스트 데이터에서 잘 동작하는 거리 척도이다.
K-평균 클러스터링 알고리즘
- 평균을 이용해 데이터 포인트간 거리를 계산하고, 이를 통해 k개의 클러스터를 형성하는 알고리즘
- 클러스터 개수 k는 외부 알고리즘을 사용해서 결정하거나, 문제의 맥락에 따라 분석자가 직접 k를 설정한다.
- k 값을 어떻게 설정해야 할지 불분명한 경우, 시행착오(trial & error)를 반복하거나 휴리스틱 기반 알고리즘을 통해 적절한 수의 클러스터를 결정해야 한다.
- 클러스터 중심점을 이용해 데이터 포인트의 클러스터가 결정되는 하향(top-down) 방식이다.
K-평균 클러스터링 알고리즘 장점
- 다른 알고리즘에 비해 클러스터링 방식이 간단하다.
- 빠르고 확장성이 좋아 인기가 많다.
- 대규모 데이터셋을 빠르게 처리할 수 있다.
K-평균 클러스터링 알고리즘 단점
- 적절한 클러스터의 개수를 정하기 어려울 수 있다.
- 클러스터 중심점을 초기에 무작위로 설정함. 이에 따라 알고리즘 실행마다 클러스터링 결과가 달라질 수 있다.
- 각 데이터 포인트는 하나의 클러스터에만 할당된다.
- 이상치에 취약하다.
K-평균 클러스터링 알고리즘 로직
초기 설정
- 클러스터 개수(k) 를 설정한다.
- 사용할 거리 측정 방식을 정한다.
- 데이터 셋에 이상치가 포함된 경우, 기준에 따라 이상치를 제거한다.
실행 단계
- 데이터 포인트 중 k개를 골라 클러스터 중심점으로 설정한다.
- 각 데이터 포인트들과 k개의 클러스터 중심점 간 거리를 계산한다.
- 각 데이터 포인트를 가장 가까운 클러스터 중심점인 그룹에 할당한다.
- 각 그룹의 중심점을 그룹 내 포인트들의 중심점으로 재할당한다.
- 3.과 4. 과정을 반복한다. 다음 조건이 만족하면 반복을 종료한다.
- 그룹의 중심점이 더이상 변하지 않는다.
- 알고리즘이 최대 반복 횟수(m_{max})를 초과한다.
- 알고리즘 실행 시간이 최대 실행 시간(t_{max})를 초과한다.
K-평균 클러스터링 알고리즘 파이썬 구현
# 1. 필요 라이브러리 load
from sklearn import cluster
import pandas as pd
import numpy as np
# 2. 데이터셋 생성
dataset = pd.DataFrame(
{'x': [11, 21, 28, 17, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 62, 70, 72, 10],
'y': [39, 36, 30, 52, 53, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 18, 7, 24, 10]
})
# 3. 클러스터 인스턴스 생성 및 데이터 학습
myKmeans = cluster.KMeans(n_clusters = 2)
myKmeans.fit(dataset)
# 클러스터 결과(라벨과 중심점)
labels = myKmeans.labels_
centers = myKmeans.cluster_centers_
# 결과 출력
print(labels)
>> [1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1]
print(centers)
>> [[62.16666667 15.66666667]
[33.78571429 50. ]]
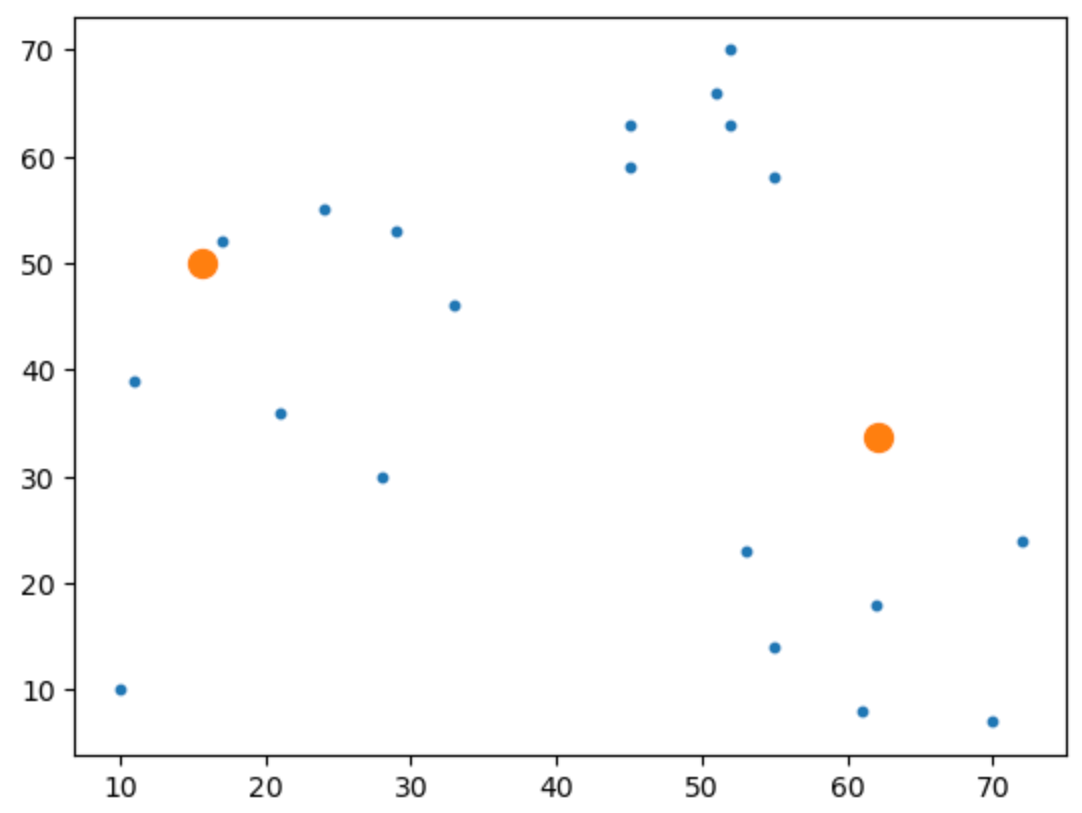
# 클러스터링 결과 시각화
import matplotlib.pyplot as plt
plt.scatter(dataset['x'], dataset['y'], s = 10)
plt.scatter(centers[0], centers[1], s = 100)
plt.show()
위 클러스터 결과 시각화의 결과는 다음과 같다.
계층적 클러스터링 알고리즘(hierarchical clustering)
- 비슷한 데이터 포인트끼리 묶어서 점진적으로 클러스터 중심점으로 이동한다.
- 개별 데이터 포인트부터 클러스터를 형성해 나가는 상향(bottom-up) 방식이다.
계층적 클러스터링 알고리즘 단계
- 먼저 각 데이터 포인트마다를 클러스터로 간주한다. 만약 데이터 포인트가 100개 있으면, 클러스터 100개로 볼 수 있다.
- 서로 가장 가까이에 위치한 클러스터끼리 큰 클러스터로 묶는다.
- 특정 종료 조건이 만족하는지 확인하고, 만족하지 않으면 2번 단계를 반복한다.
- 종료 조건은 클러스터의 수, 클러스터 내 거리 등 여러가지 조건이 있을 수 있다.
덴드로그램(dendrogram)
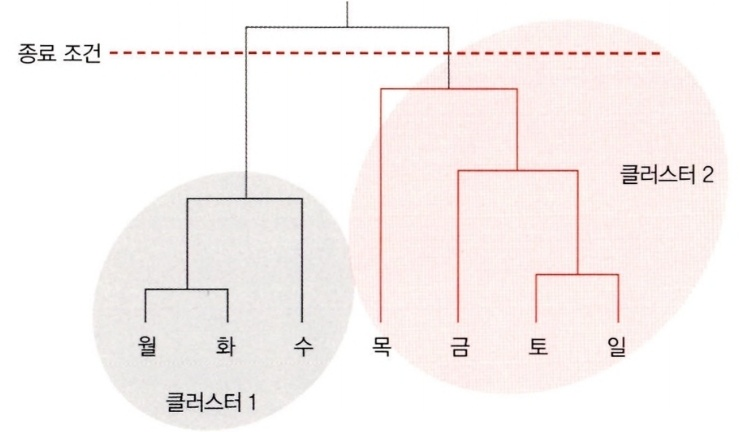
- 알고리즘을 통해 클러스터의 구조를 덴드로그램으로 표현할 수 있다.
- 덴드로그램의 수직선 높이는 데이터 포인트간 거리를 표현한다.
계층적 알고리즘 코딩하기
# 1. 필요 라이브러리 load
from sklearn.cluster import AgglomerativeClustering
import pandas as pd
import numpy as np
# 2. 데이터셋 정의
dataset = pd.DataFrame(
{'x': [11, 21, 28, 17, 29, 33, 24, 45, 45, 52, 51, 52, 55, 53, 55, 61, 62, 70, 72, 10],
'y': [39, 36, 30, 52, 53, 46, 55, 59, 63, 70, 66, 63, 58, 23, 14, 8, 18, 7, 24, 10]
})
# 3. 계층적 클러스터 형성 및 클러스터 학습
cluster = AgglomerativeClustering(n_clusters = 2, affinity = 'euclidean', linkage = 'ward')
cluster.fit_predict(dataset)
# 4. 클러스터 형성 결과 출력
print(cluster.labels_)
>> [0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0]
클러스터 평가하기
클러스터링은 서로 다른 특성을 지닌 데이터 포인트들을 각 클러스터에 잘 분리하는 것이 목표다.
클러스터링의 목표
- 같은 클러스터에 할당된 데이터 포인트들은 서로 비슷해야 한다.
- 다른 클러스터에 할당된 데이터 포인트들은 서로 달라야 한다.
클러스터링 평가
- 정성적 평가: 시각화를 통해 육안으로 클러스터링 결과를 평가
- 정량적 평가: 수학적 방법으로 클러스터링 성능을 정량화
- 실루엣 분석
실루엣 분석(silhouette analysis)
- 클러스터 내 포인트가 얼마나 서로 뭉쳐있고, 클러스터 간에는 얼마나 분리돼 있는지 평가하는 기법
- 특정 클러스터의 각 데이터 포인트가 다른 클러스터에 속한 포인트들과 얼마나 가까운지 나타내는 plot을 그림
- 실루엣 점수는 [0, 1] 사이에 위치하며 아래와 같이 해석된다.
| 값 | 범위 | 클러스터링 품질 설명 |
| 0.71 - 1.0 | 상 | 클러스터간 분리가 매우 잘됨 |
| 0.51 - 0.70 | 중 | 클러스터간 어느정도 분리가 됨 |
| 0.26 - 0.50 | 하 | 클러스터가 형성은 되나 결과 신뢰가 어려움 |
| < 0.25 | 데이터 내 클러스터가 존재하지 않음 | 해당 데이터로 클러스터링을 하는데 실패함 |
- 각 클러스터마다 다른 실루엣 점수를 가지며, 데이터 포인트가 잘못된 클러스터에 할당된 경우 실루엣 점수가 최하 -1까지 가질 수도 있다.
클러스터링 활용 사례
데이터 셋에 숨겨진 패턴을 찾기 위해 클러스터링을 사용할 수 있으며, 아래 사례에서 적용될 수 있다.
- 범죄 다발생 지역 분석
- 인구 통계 및 사회 분석
- 시장 세분화
- 타게팅 광고
- 고객 카테고리 분석
6-3. 차원 축소 알고리즘 이해하기
데이터의 특성
- 데이터의 각 특성은 문제 공간의 차원에 대응된다.
- 문제 공간의 차원이 너무 크면 데이터를 해석하거나 이해하기 어려워진다.
차원 축소(dimensionality reduction)
- 특성의 개수를 최소화해 문제를 단순화하는 방법
- 차원 축소는 다음과 같은 방식으로 실행한다.
- 특성 선별(feature selection): 풀려눈 문제 맥락에 맞는 중요한 특성들만 선택하는 방법
- 특성 조합(feature aggregation): 둘 이상의 특성을 조합해 차원을 축소하는 방법
- 주성분 분석(PCA): 선형 비지도 학습 알고리즘
- 선형 판별 분석(Linear Discriminant Analysis, LDA): 선형 지도 학습 알고리즘
- 커널 주성분 분석(kernel PCA): 비선형 알고리즘
주성분 분석(PCA)
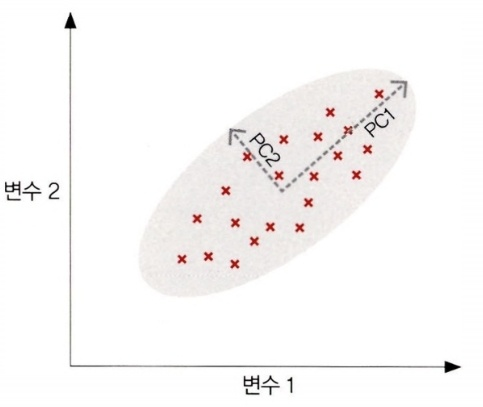
- 선형 결합을 이용해 차원을 축소하는 비지도 학습 기법이다.
- 여러 변수들을 가장 잘 설명하는 축들을 새로운 변수로 설정한다.
- 새로운 변수들로 기존 데이터의 위치들을 표현한다.
- 차원 축소 시 많이 사용되는 알고리즘이다.
PCA 실행 코드
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
iris = load_iris()
X = pd.DataFrame(iris['data'], columns = iris['feature_names'])
pca = PCA(n_components = 4)
pca.fit(X)
pca_df = pd.DataFrame(pca.components_, columns = X.columns,
index = ['pc1', 'pc2', 'pc3', 'pc4'])
pca_df
결과는 다음과 같다.
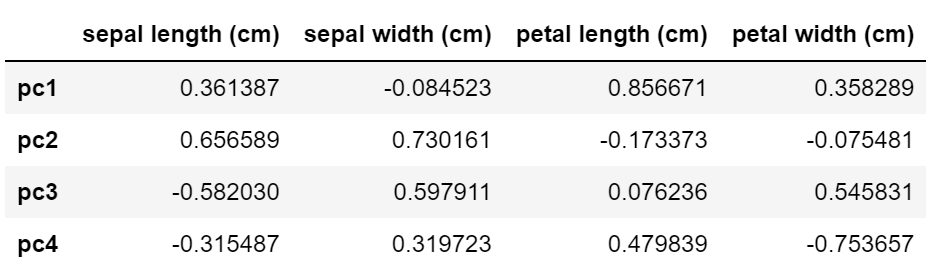
- 일반적으로 새로운 변수들(pc1 ~ pc4)은 기존 변수들의 개수와 동일한 수로 생성된다.
- 각 주성분들 (pc1 ~ pc4) 은 원래 변수의 조합으로 생기는 새로운 변수들이다.
- iris 데이터의 각 point들을 주성분의 축으로 아래와 같이 변경할 수 있다.
colnames = X.columns
for idx in range(1, 5):
x_mult_pca_comp = [(X[colnames[col_idx]] * pca_df[colnames[col_idx]][idx-1]) for col_idx in range(4)]
X[f'pc{idx}'] = np.array(x_mult_pca_comp).sum(0)
X
결과는 다음과 같다.
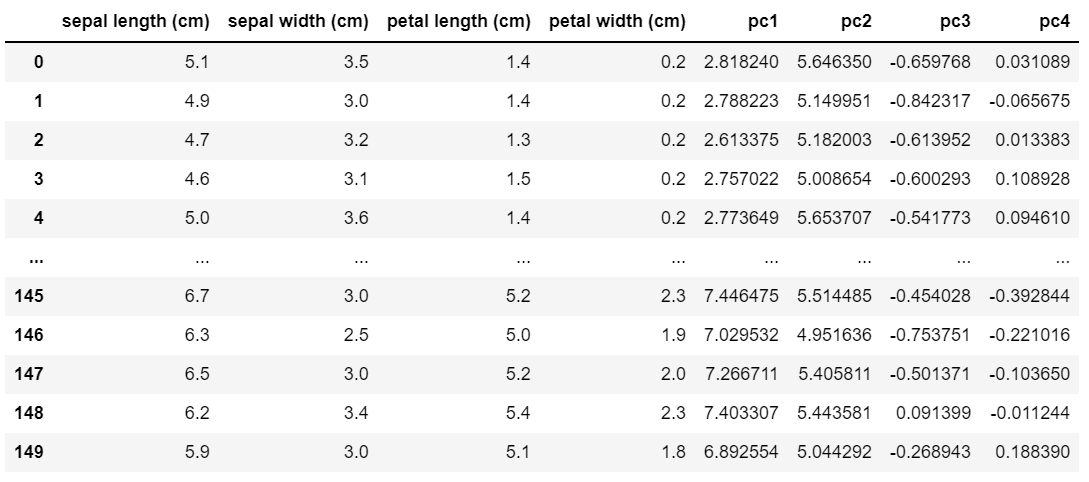
- 주성분들을 모두 사용하면 기존 변수를 똑같이 재현할 수 있다.
for col_idx in range(4):
x_pca_mult_pca_comp = [X[f'pc{idx}'] * pca_df.loc[f'pc{idx}', colnames[col_idx]] for idx in range(1, 5)]
X[f'restored_{colnames[col_idx]}'] = np.array(x_pca_mult_pca_comp).sum(0)
X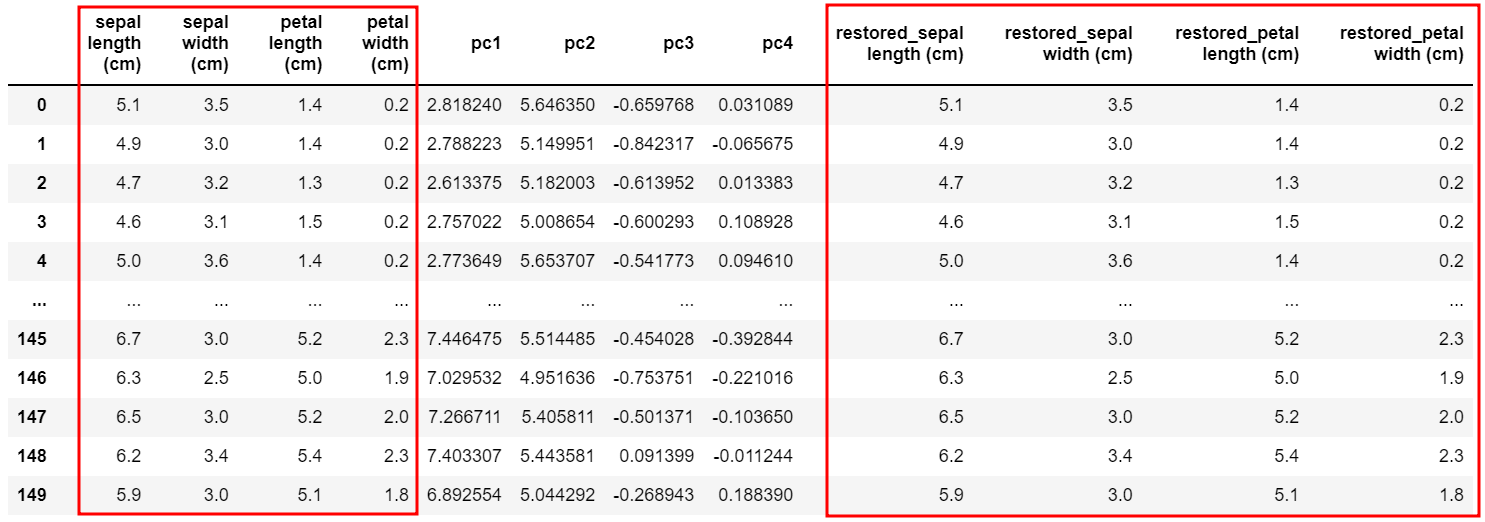
PCA의 분산 비율(variance ratio)
print(pca.explained_variance_ratio_)
>> [0.92461872 0.05306648 0.01710261 0.00521218]
분산 비율은 다음과 같이 해석할 수 있다.
- pc1으로만 4가지 원본 특성을 대체할 시, 원본 특성이 가진 분산의 92.4%를 pc1이 보존할 수 있다. 즉, 원본 데이터의 분산 근삿값이 92.4%가 된다는 것임
- pc2 를 추가적으로 사용하면, pc1만 사용할 때보다 원본 분산을 5.3% 더 보존할 수 있다.
- pc1 ~ pc4를 모두 사용하면 원본 분산의 100%를 보존한다. 하지만 4개의 주성분 모두를 사용하는 것은 차원 축소의 관점에서는 의미가 없다 (원본의 차원 수만큼 그대로 사용하는 것이기 때문).
주성분 분석의 장점
- 복잡한 특성들을 결합해 주성분을 생성한다. 특성들을 잘설명하는 주성분 일부만 사용해 차원 축소가 가능하게 한다.
- 선형적인 변수나 변수간 관계에 적합하다.
주성분 분석의 한계
- 연속형 변수만 처리가 가능하며, 카테고리 변수에는 적절한 방법이 아니다.
- 특성을 결합해 근삿값으로 처리하게 된다. 주성분 모두를 사용하지 않으면 데이터 정보 손실이 발생할 수밖에 없다.
- 변수들이 상관 관계를 형성한다는 가정이 존재한다. 변수간 상관성이 없으면 주성분을 찾아내기 어렵다.
- 비선형적인 특징을 가진 특성들에는 부적합할 수 있다. 이 때에는 로그 변환 등 전처리를 통해 비선형적인 특성을 선형적으로 변환할 필요가 있다.
6-4. 연관 규칙 마이닝 이해하기
연관 규칙 마이닝(association rules mining) 특징
- 데이터에서 발생하는 패턴의 빈도를 측정할 수 있다.
- 패턴들이 형성하는 인과 관계를 분석할 수 있다.
- 정확도를 계산해 패턴의 유용성을 정량화할 수 있다.
연관 규칙 마이닝 활용 사례
- 여러 변수들이 가진 인과 관계를 조사할 때 유용하며 아래와 같이 활용할 수 있다.
- 습도, 구름 양, 온도 요소가 다음 날 비가 내리는 것과 연관이 얼마나 있는가?
- 어떤 보험 청구 유형이 보험 사기일 가능성이 높은가?
- 어떤 약물 조합이 환자에게 합병증을 발생시킬 가능성이 있는가?
장바구니 분석(basket analysis)
- 거래 데이터에 연관 규칙 분석을 적용한 분석방법
- 거래 데이터(transaction data): 이마트 등 대형 마트의 쇼핑 기록 데이터
- 특정 아이템(품목)을 다른 아이템들과 함께 구매할 조건부 확률을 계산한다. 장바구니 분석을 통해 아래 질문들에 답할 수 있다.
- 매대에 아이템을 어떻게 진열하는게 최적의 방법인가?
- 광고지에는 어떤 아이템들을 함께 노출하는 것이 좋은가?
- 특정 아이템들과 어떤 아이템을 함께 추천하는 것이 좋은가?
장바구니 분석의 장점
- 데이터는 여러 부가 정보 없이 구매한 아이템 정보만 가지기 때문에 데이터 수집이 쉽다.
- 장바구니 분석 결과를 해석하기 쉬워 비지니스 의사결정에 사용되기 좋다.
- 위 장점들로 다양한 매스 마켓 리테일(mass-market retail) 기업에서 활용하는 분석기법이다.
장바구니 분석에 연관 규칙 적용하기
거래 데이터에 담긴 아이템들간 관계를 수학적으로 표현하기
- X 아이템들 (sushi, pizza) 을 구매한 사람들이 Y 아이템들 (coke) 도 구매한다.
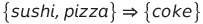
- X 아이템들과 Y 아이템들은 서로 겹치지 않아야 한다.

연관 규칙의 종류
- 사소한 규칙
- 모두가 아는 사실이 도출되서 활용 가치가 없는 경우
- 신뢰도가 높더라도 아주 상식적인 사실들이기 때문에 의사결정으로 이어지기 어려움
- 이런 규칙들은 무시해도 상관없음
- ex> 사람은 100층 건물에서 떨어진 경우 99%가 죽는다 등
- 해석 불가능한 규칙
- 이벤트 X가 이벤트 Y로 어떻게 이어지는지 해석이 어려운 케이스
- 실제로 규칙을 활용하기 어렵다. 도출된 규칙을 이해해야 전략을 구상할 수 있기 때문이다.
- 실행 가능한 규칙
- 연관 규칙 마이닝으로 도출하고자 하는 규칙
- 규칙은 사람이 이해할 수 있고 중요한 인사이트를 담고 있다.
- 해당 비지니스에 지식이 있는 담당자들과 함께 규칙을 이용해 다양한 활용 방안을 찾을 수 있다.
- ex> 물품 A를 산 사람들이 물품 B의 구매로 이어지는 패턴이 있을 때 >> 물품 A와 물품 B간 상품 배치를 가깝게 함
평가 척도
1. 지지도(support)
- 해당 패턴이 데이터셋에서 얼마나 자주 등장하는지 여부
- 대상 규칙의 발생 빈도를 전체 거래 기록 개수로 나누어서 표현한다.
- 패턴 발생 빈도가 클수록 지지도는 높고, 패턴 발생이 희귀할수록 지지도는 낮다.
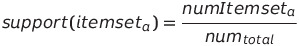
2. 신뢰도(confidence)
- 조건부 확률을 이용해 이벤트 X와 이벤트 Y간 얼마나 강한 연관이 존재하는지 정량화한 척도
- 이벤트 X가 발생했을 때, X의 발생이 Y로 이어질 조건부 확률을 의미한다.
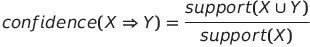
3. 향상도(lift)
- 조건 X를 이용해서 예측했을 때, 무작위로 Y를 예측하는거보다 예측 개선 효과가 얼마나 큰지 표현하는 척도
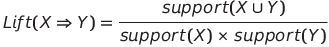
연관 규칙 마이닝 알고리즘
Apriori 알고리즘
- 여러 단계를 반복적으로 실행해 연관 규칙을 생성하는 알고리즘
- 생성과 테스트(generation-and-test) 접근 방식을 수행함
- 알고리즘은 두 단계로 정의됨
- 후보 생성 단계: 여러 후보 세트를 생성한다. 여기서 각 세트들의 지지도는 지지도 threshold를 넘어야 한다.
- 필터링 단계: 신뢰도 threshold보다 낮은 규칙들을 제거한다.
- 필터링 후 남은 규칙이 알고리즘의 결과가 됨
Apiriori 알고리즘 한계
- 후보 생성 단계에서 병목이 크게 발생한다.
- 전체 아이템 수가 n개라면 가능한 아이템의 수는 2^n개 이다 (세트에 포함되거나, 안되거나).
- 따라서 아이템 수가 많은 경우에는 Apiriori 알고리즘이 적합하지 않다.
FP-growth 알고리즘
- Apiriori 알고리즘의 개선 버전
- 빈출 패턴 성장(frequent pattern growth) 방식으로 알고리즘이 수행됨
- FP-트리 생성
- 빈출 패턴 마이닝
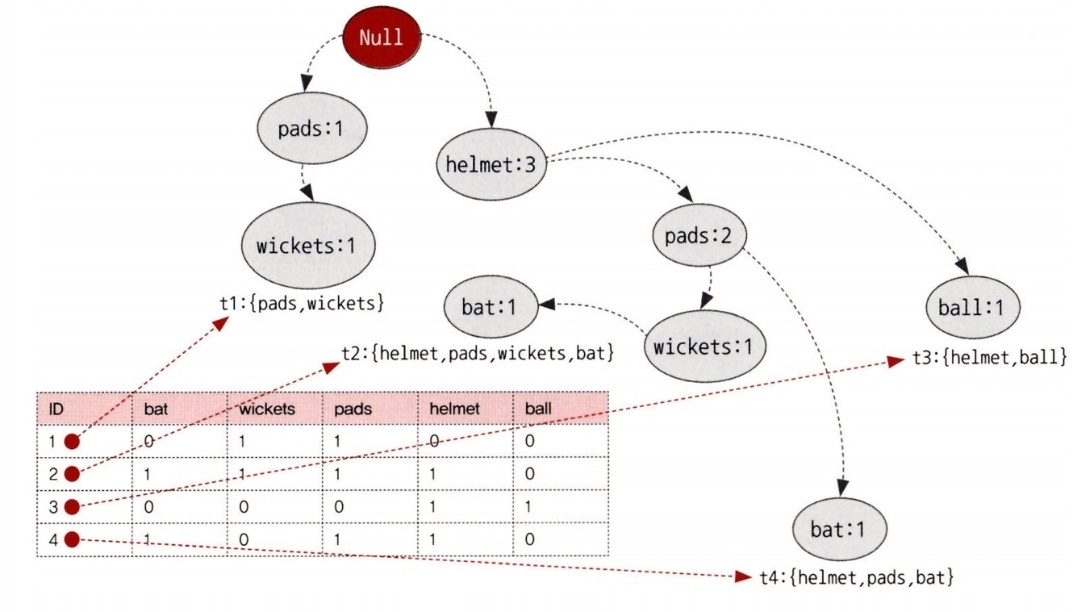
FP-트리 생성
- 각 아이템의 발생 빈도를 계산하고 내림차순으로 정렬한다.
- 각 아이템의 발생 빈도를 기준으로 각 거래 기록 아이템을 내림차순으로 정렬한다.
- 이를 순서 트리 형태로 아이템을 표현한다 (루트노드는 Null이다).
빈출 패턴 마이닝
- FP-트리에서 자주 발생하는 패턴을 추출한다.
- 순서 트리 구조를 이용했기 때문에 발생 빈도가 높은 패턴을 효율적으로 쉽게 탐색할 수 있다.
- 리프 노드에서 위로 이동하면서 조건부 규칙을 계산할 수 있다.
FP-growth 코드
# 라이브러리 설치
# !pip install pyfpgrowth
import numpy as np
import pandas as pd
import pyfpgrowth as fp
# 데이터 생성
dict1 = {
'id': [0, 1, 2, 3],
'items': [['wickets', 'pads'],
['bat', 'wickets', 'pads', 'helmet'],
['helmet', 'pads'],
['bat', 'pads', 'helmet']]
}
transactionSet = pd.DataFrame(dict1)
# 규칙 생성 및 최소 빈도(1) 입력
patterns = fp.find_frequent_patterns(transactionSet['items'], 1)
patterns
>> {('wickets',): 2,
('pads', 'wickets'): 2,
('bat', 'wickets'): 1,
('helmet', 'wickets'): 1,
('bat', 'pads', 'wickets'): 1,
('helmet', 'pads', 'wickets'): 1,
('bat', 'helmet', 'wickets'): 1,
('bat', 'helmet', 'pads', 'wickets'): 1,
('bat',): 2,
('bat', 'helmet'): 2,
('bat', 'pads'): 2,
('bat', 'helmet', 'pads'): 2,
('helmet',): 3,
('helmet', 'pads'): 3,
('pads',): 4}
신뢰도가 0.3 이상인 규칙만 선별하기
rules = fp.generate_association_rules(patterns, 0.3)
rules
>> {('pads',): (('helmet',), 0.75),
('wickets',): (('bat', 'helmet', 'pads'), 0.5),
('bat',): (('helmet', 'pads'), 1.0),
('helmet',): (('pads',), 1.0),
('bat', 'pads'): (('helmet',), 1.0),
('bat', 'wickets'): (('helmet', 'pads'), 1.0),
('pads', 'wickets'): (('bat', 'helmet'), 0.5),
('helmet', 'pads'): (('bat',), 0.6666666666666666),
('helmet', 'wickets'): (('bat', 'pads'), 1.0),
('bat', 'helmet'): (('pads',), 1.0),
('bat', 'helmet', 'pads'): (('wickets',), 0.5),
('bat', 'helmet', 'wickets'): (('pads',), 1.0),
('bat', 'pads', 'wickets'): (('helmet',), 1.0),
('helmet', 'pads', 'wickets'): (('bat',), 1.0)}- 각 규칙은 콜론(:) 왼쪽과 오른쪽으로 구분된다.
- 개별 규칙의 지지도도 함께 출력된다.
6-5. 활용 사례 - 비슷한 트윗끼리 클러스터링하기
비지도 학습을 통해 실시간으로 비슷한 트윗을 묶는데 사용할 수 있다.
- 토픽 모델링: 주어진 트윗 집합에서 여러 주제를 도출한다.
- 클러스터링: 도출한 주제를 트윗에 연결 짓는다.
토픽 모델링(topic modeling)
- 문서 집합 내에서 분류에 사용할 수 있는 개념을 도출하는 프로세스이다.
- 잠재 디리클레 할당(LDA, Latent Dirichlet Allocation)가 많이 사용된다.
- 토픽 모델링을 통해 트위터 뭉치를 분류할 수 있는 적당한 주제를 찾아낼 수 있다.
- 트윗의 경우는 최대 144자로 짧은데다 특정 주제를 다루는 경우가 많아 LDA보다 간단한 알고리즘으로도 토픽 모델링이 가능하다.
트윗 토픽 모델링 알고리즘 과정
- 트윗을 토큰화(tokenize) 한다.
- 데이터를 전처리한다. 문자 속 불용어, 숫자, 기호를 지우고 어간을 추출(stemming)한다.
- 트 데이터로 단어-문서-행렬 (TDM, Term-Document-Matrix)을 생성한다. 중복을 제거한 트윗에서 가장 흔히 등장하는 200개 단어를 선택한다.
- 개념이나 주제를 직간접적으로 대표하는 단어 10개를 선정한다. 문서에서 발견한 10개 단어는 트윗 클러스터링 중심에 위치하는 주제 단어가 된다.
클러스터링
- 도출한 주제를 클러스터링의 중심점으로 선택한다.
- 이후 K-평균 클러스터링 알고리즘을 실행하여 각 트윗을 연관된 클러스터에 할당한다.
6-6. 이상 탐지 알고리즘 이해하기
이상 탐지 알고리즘
- 이상치(anomaly point): 데이터 속 일반적인 관측들과 다르게 비정상적이거나 특이한 패턴을 띄는 포인트
- 이상 탐지(anomaly detection) 알고리즘: 이상치를 찾아내는 알고리즘
이상 탐지 알고리즘 활용 분야
- 신용 카드 사기 범죄 탐지
- MRI(자기공명영상) 스캔 사진 또는 영상에서 악성 종양 탐지
- 네트워크 클러스터 시스템 장애 탐지 및 대응
- 고속도로에서 교통 사고 탐지
이상탐지 알고리즘 종류
- 클러스터링 알고리즘
- 클러스터링에서 특정 임곗값을 넘어가는 데이터 포인트들을 이상치로 판별
- 한계: 결과가 편향돼 탐지 정확도나 유용성에 영향을 줄 수 있다.
- 밀도 기반 이상 탐지 알고리즘 (density-based)
- 밀집된 이웃들에서 멀리 떨어진 데이터 포인트를 이상치로 판별함
- K-최근접 이웃 알고리즘 (K-Nearest Neighbors, KNN) 등이 있음
- 서포트 벡터 머신 알고리즘 (SVM)
- 데이터 포인트의 경계를 학습함
- 경계 밖에 위치한 데이터 포인트들을 이상치로 식별함
'Study > 알고리즘' 카테고리의 다른 글
| 프로그래머가 알아야 할 알고리즘 40 Chapter 5 그래프 알고리즘 (4) | 2022.11.16 |
|---|---|
| 프로그래머가 알아야 할 알고리즘 40 Chapter 4 알고리즘 설계 (6) | 2022.11.14 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 3 알고리즘에 사용되는 자료구조 (4) | 2022.10.31 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 2 알고리즘에 사용되는 자료구조 (1) | 2022.10.23 |
| 프로그래머가 알아야 할 알고리즘 40 Chapter 1 알고리즘 기초 (0) | 2022.10.21 |